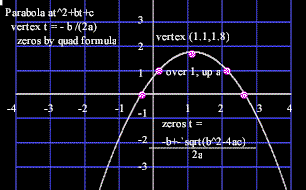
A quadratic function y = a t^2 + b t + c has a parabolic graph, possibly crossing the x axis at points which can be determined by the quadratic formula (these points, if they exist, are called zeros of the function or the graph), with a vertex at another point indicated by the quadratic formula. The vertex is the highest or lowest point on the parabola, depending on whether it opens upward or downward. Moving to the right or left of the vertex a distance of 1 unit, we move vertically a distance of a units.
The figure below summarizes these behaviors. The discussion and exercises that follow will clarify these ideas.

Once you have mastered these ideas, you will be able to easily graph any given quadratic function and determine many useful characteristics of quadratic models.
Parabolas and Quadratic Functions
The shape of the graph of a quadratic function y = ax^2 + bx + c is a parabola. A parabola is a very specific shape. It is traditionally defined to be the set of points equidistant from a specific point (called the focus) and a straight line (called the directrix), and this is a good definition. However, you don't have to know this now.
Right now you need to know that a parabola can be defined as the shape of the graph of y = x^2, or any shape that can be obtain by stretching this graph uniformly in the y and/or the x direction. Parabolas can also be rotated by rotating the y axis through an angle between 0 and 360 degrees, or shifted in the x direction (right or left) or in the y direction (up or down).
Graph of the Basic y = x^2 ParabolaThe graph of y = x^2 can easily be constructed by first making a table of values:
x
y = x^2
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
The point-to-point graph of this table is depicted below:
The lines between the points of this graph are straight. They don't really depict the graph of y = x^2 accurately, except at the marked graph points corresponding to the points on the table.
A more accurate graph of y = x^2 for x=-3 to 3 is depicted below:
The low point of this parabola is called its vertex. If the parabola was turned upside down, or even rotated at some angle, this point would still be easy to identify as the 'blunt tip' of the parabola.
The vertex of the y = x^2 parabola is (0,0).
If the graph is stretched by factor 3 in the vertical direction, so each point moves 3 times as far from the x axis, it might end up looking like the graph below:
Both of the above graphs have the shapes of parabolas.
A parabola can be stretched in the vertical direction by a factor of 2 or 3 or more. These stretches will move points 2 or 3 times as far from the x axis, and will therefore tend to make the parabola look taller. In this case the parabola will be either twice as tall or 3 times as tall.
If we vertically stretched the parabola by a factor of 1, it would become 1 times as tall, so it wouldn't change. If a parabola was vertically stretched by a factor of .5, it would become .5 times as tall. In this case it would actually be compressed. A vertical stretch by a factor greater than 1 moves points further from the y axis and therefore makes a parabola taller, while a vertical stretch by a factor less than 1 makes it shorter, thereby compressing it.
The figure below shows a series of parabolas with various vertical stretches, some greater than 1 and some less than 1.
The parabola below has been slightly compressed and moved to the left and down. Its vertex has shifted from (0,0) to (-.7,-.7). This moves every point by -.7 units in the x direction and by -.7 units in the y direction.
A parabola can also be stretched by a negative factor. For example a stretch of -1 would make the parabola -1 times as tall, which can be thought of as turning it upside down. The parabola below has been stretched by a negative factor, and its vertex has been shifted as indicated.
When we look at part of a parabola we don't always recognize it as a parabola. The figure below shows part of a parabola, but it doesn't show enough to see its overall shape. This parabola has been compressed so much that it doesn't curve much, at least in the window we are viewing. If we 'zoom back' far enough we can see the overall shape and locate the vertex.
It turns out that there are techniques for determining from its points whether a given graph is part of a parabola. One way, of course, is to pick three points on the original graph and do a quadratic model. If the quadratic function has a graph that coincides with that of the original graph, then the original graph is a parabola. We will see other techniques later.
As we said earlier, the graph of a quadratic function y = ax^2 + bx + c is a parabola. In fact it is a vertical parabola, and can be obtained by vertically stretching the graph of y = x^2, then shifting it right or left and up or down. It is also the case that if a graph is a vertical parabola, it must be the graph of some quadratic function.
The statements made in the preceding paragraph deserve further consideration. One thing said above is
The graph of a quadratic function is a vertical parabola, and any vertical parabola is the graph of a quadratic function.
This statement asserts that to say a graph is a vertical parabola is identical to saying that it is a graph of a quadratic function, that the two characterizations of a graph are identical, that being the graph of a vertical parabola and being the graph of a quadratic function are completely equivalent.
This can be stated logically and succinctly as follows
A graph is a graph of a vertical parabola if, and only if, it is a graph of some quadratic function.
Note that this doesn't tell us how to find that precise quadratic function. It just guarantees that such a function exists.
Of course, we already know how to find the function by fitting three graph points. If we fit a quadratic function to 3 points of a graph, and if the graph of the function is identical to that of the graph, then the original graph was a parabola.
The graph of a specific quadratic function y = a x^2 + b x + c has several important characteristics, most of which can be understood in terms of the quadratic formula:
As an example, consider the graph of the function y = x^2 - 3x - 4.
The vertex of the graph is at xVertex = - b / (2a) = - (-3) / (2 * 1) = 3/2.
The corresponding y coordinate is found by substituting x = 3/2 into the definition of the function:
yVertex = (3/2)^2 - 3(3/2) - 4 = 9/4 - 9/2 - 4 = 9/4 - 18/4 - 16/4 = -25/4.
Thus the vertex is at (3/2, -25/4) or, in decimal form, (1.5,-6.25).
The graph crosses the x axis when y is zero. By the statement of the quadratic formula, this occurs when x^2 - 3x - 4 = 0. This equation is in the form specified by the formula, with a = 1, b = -3 and c = -4. By the statement of the formula, the zero value is at
x = [ - (-3) +- `sqrt( (-3)^2 - 4(1)(-4) ) ] / (2 * 1) = [ 3 +- `sqrt(25) ] / 2 = [3 +- 5] / 2.
The two solutions are therefore
x = [3 + 5] / 2 = 8/2 = 4
and
x = [3 - 5] / 2 = -2 / 2 = -1.
So the graph crosses the x axis at x = 4 and at x = -1.
Notice that the vertex, at x = 3/2, is exactly halfway between these zeros. (You should verify this for yourself). It has to be there because the parabola is symmetric about a vertical line through its vertex.
This is always the case when a quadratic function has two zeros. The vertex lies on a vertical line halfway between the zeros.
The reason for this is right there in the quadratic formula. Halfway between -b + `sqrt(b^2-4ac) and -b - `sqrt(b^2-4ac) is just plain -b. So halfway between the two points [-b +- `sqrt(b^2-4ac) ] / (2a) is just -b / (2a), which is where the vertex is.
If we make a table with x values 1, 2 and 3 units to the left and right of the vertex value xVertex = 3/2 = 1.5, we obtain
Table for y = x^2 - 3x - 4
x
y
-1.5
2.75
-0.5
-2.25
0.5
-5.25
1.5
Vertex
-6.25
2.5
-5.25
3.5
-2.25
4.5
2.75
The symmetry is clear from the fact that the same numbers appear on the left as on the right, at the same distances from x = 1.5.
If we move 1 unit to the right or to the left of the vertex, as the table shows, we move 1 unit vertically. We start at the vertex value of - 6.25 and go up unit to - 5.25.
If we graph this function on the same scale as the y = x^2 function, it will have exactly the same shape. This is obvious from the way the numbers on the table act. In both cases, if we move 1 unit from the vertex in the x direction we go up 1 unit; if we move 2 units in the x direction from the vertex we go up 4 units; moving 3 units from the vertex in the x direction takes us up 9 units.
Example 2: y = 2x^2 - 12x + 18.As a second example consider the function y = 2x^2 - 12x + 18. For this function, we have a = 2, b = -12 and c = -18.
The vertex of the graph is
xVertex = -b / (2a) = - (-12) / (2 * 2) = 12 / 4 = 3.
The corresponding y coordinate is again found by substituting the x coordinate into the function. We obtain
yVertex = 2(3)^2 - 12(3) + 18 = 2(9) - 36 + 18 = 0.
The vertex therefore occurs at (3,0).
The graph meets the x axis where y=0. Of course we just saw that the vertex has y coordinate 0, so we know that y = 0 when x = xVertex = 3. From the statement of the quadratic formula, we also know that y is 0 when x = [ -(-12) +- `sqrt((-12)^2 - 4(2)(18)) ] / (2 * 2). Now the quadratic formula says that these are the only x coordinates for which y = 0. So x = xVertex = 3 had better be among the solutions of the quadratic formula.
Evaluating the quadratic formula we obtain
x = [ -(-12) +- `sqrt((-12)^2 - 4(2)(18)) ] / (2 * 2)
= [ 12 +- `sqrt(144-144) ] / (2*2)
= [12 +- 0 ] / 4
= 12/4
= 3.
Since the square root is 0, it doesn't make any difference whether we use the + or the - of the +- . In either case we obtain x = 3, which coincides with the x coordinate of the vertex. This is no coincidence, since the 12/4 we end up with is just -b / (2a). Any time the square root is 0, this is what we end up with.
So the graph of y = 2x^2 - 12x + 18 meets the x axis only at the vertex. This x value occurs twice as the solution to the quadratic equation, so we sometimes call it a zero of multiplicity 2.
If we move 1 unit to the right or the left of the vertex, we go up a = 2 units. So moving 1 unit to the right of (3,0) and 2 units up we end up at x = 3+1 = 4 and y = 0+2 = 2, at the point (4,2). Similarly moving 1 unit to the left of (3,0) and 2 units up we end up at (2,2).
We could in fact make a table with x values centered at the vertex. Such a table is given below:
Table for y = 2 x^2 - 12 x + 18
x
y
0
18
1
8
2
2
3
0
4
2
5
8
6
18
Note that the y values on the table are the same as those we would obtain for the function y = 2x^2, for x = -3, -2, -1, 0, 1, 2, 3 (you should take a minute to figure out both tables to confirm this for yourself). So we see that this graph is just the same as the y = 2x^2 graph, with the vertex shifted over to (3,0).
The graph of the 3 central points, and the graph of the function, are shown below:
We see that when `sqrt(b^2 - 4ac) = 0, the solutions to the quadratic equation are both the same, both equal to -b / (2a). In this case the vertex is the only point where the graph touches the x axis. We call this a zero of multiplicity 2.
Example 3: y = -3x^2 + 2x - 2.
As a third example we consider y = -3x^2 + 2x - 2. For this parabola, a = -3, b = 2 and c = -2.
The vertex is at -b / (2a) = -2 / (2 * -3) = 2 / 6 = 1/3.
The y coordinate of the vertex is therefore at
yVertex = -3 (1/3)^2 + 2(1/3) - 2 = -3(1/9) + 2/3 - 2 = -1/3 +2/3 -6/3 = -5/3.
The vertex is thus located at (1/3, -5/3) = (-.333..., -1.666...)
The points 1 unit to the right and left of the vertex are located vertically -3 units from the vertex:
1 unit to the right: (1/3 + 1, -5/3 - 3) = (4/3, -14/3) = (1.33...,-4.66...)
1 unit to the left: (1/3 - 1, -3 - 3) = (-2/3, -14/3) = (-.66..., -4.66...)
These points, and the rest of the graph, are indicated below:
It is clear that this parabola never crosses the x axis. The quadratic formula had better confirm this.
The quadratic formula tells us that y = 0 when
x = [ -2 +- `sqrt( 2^2 - 4(-3)(-2) ] / (2 * -3) = [ -2 +- `sqrt ( -20 ) ] / -6.
This looks fine until we try to take the square root of -20. There is no real number we can square to get a negative number, since squaring any real number gives us a positive. Therefore there is no real number that is the square root of -20.
This tells us that there is no such x as the above.
Since the statement of the quadratic formula tells us that y = 0 if and only if x is as stated above, it follows that there is no point on the graph where y = 0. This, of course, confirms what we already know. The graph never crosses the x axis.
Exercises 1-31. Graph y = x^2:
Construct a graph of y = x^2. Begin with a table using x = -3, -2, -1, 0, 1, 2, 3.
Sketch the graph that would be formed if your graph of y = x^2 was stretched vertically by a factor of 2, by a factor of 3, by a factor of .5 and by a factor of -.3.
2. Location of the vertex and fundamental points:
Determine the location of the vertex of each of the following quadratic functions:
y = x^2 + x + 1
y = x^2 + 2x + 1
y = x^2 + 3x + 1
y = x^2 + 4x + 1
y = -2 x^2 + 4x + 3
Sketch a graph for each function showing 3 points: the vertex and the points 1 unit to the right and 1 unit to the left of the vertex.
Sketch the graph of each function, based only on the 3 points you have sketched and your knowledge that the graph is a parabola.
3. Zeros of a quadratic function:
Use the quadratic formula to find the zeros of each of the functions in the above exercise. Note that some functions will not have any zeros, some will have 1 zero and some will have two.
For each function sketch on the graph the points corresponding to each of these zeros, and determine whether the graph you have sketched is consistent with the location of these zeros.
For each of your graphs, comment of the statement that the vertex lies halfway between the zeros.
If you were to draw a smooth curve passing through the vertex of each of the first four graphs, what can you say about the shape of the curve?