A power p proportionality between x and y is a function y = a x ^ p. You have just worked through a few examples of power function proportionalities.

A more common notation uses k rather than a to represent the proportionality. So we will often use y = k x ^ p to represent a power p proportionality between x and y.

Example: As an example, suppose that a builder constructs sheds of various sizes, but with the exactly the same shape and design. Clearly the amount of paint required to paint a shed depends on its size. Larger sheds will require more paint.

Suppose that the sheds come in sizes that are described by the length of their longest side, and that we know from experience that a 12-foot shed is going to require 2.4 gallons of paint. We wish to determine the amount of paint required for 10-foot, 16-foot, 20-foot and 24-foot sheds.

Suppose that the builder knows that the amount of paint is proportional to the square of the building's length. That is, the proportionality relating y = amount of paint to x = length of side is of the form y = k x ^ 2. (We will see below why this proportionality is valid).

The mathematical situation is therefore as follows:

We have the data point (x, y) = (12 feet, 2.4 gallons).

We believe that the proportionality is y = k x ^ 2.

We wish to determine y for x = 10, 16, 20 and 24 feet.

All we need to obtain our function for [y = amount of paint] is the value of the parameter k.

We easily find k by substituting our data point into the form y = k x ^ 2:

2.4 gallons = k (12 feet)^2, so

k = 2.4 gallons / (12 ft)^2 = 2.4 gallons / (144 ft^2) = .0166... gal / ft^2.

Our function is therefore

amount of paint = y = [.0166.. gal / ft^2] x^2.

To obtain the desired amounts of paint we substitute the given values of x:

When x = 10 feet,

amount of paint = y = [.0166... gal / ft^2] x^2

= [.0166... gal / ft^2] (10 ft)^2

= [.0166... gal / ft^2] (100 ft^2)

= 1.66 gal.

When x = 16 feet,

amount of paint = y = [.0166... gal / ft^2] x^2

= [.0166... gal / ft^2] (16 ft)^2

= [.0166... gal / ft^2] (256 ft^2)

= 4..27 gal.

When x = 20 feet,

amount of paint = y = [.0166... gal / ft^2] x^2

= [.0166... gal / ft^2] (20 ft)^2

= [.0166... gal / ft^2] (400 ft^2)

= 6.66 gal.

When x = 24 feet,

amount of paint = y = [.0166... gal / ft^2] x^2

= [.0166... gal / ft^2] (24 ft)^2

= [.0166... gal / ft^2] (576 ft^2)

= 8.54 gal.

1. The storage capacity of a box of a certain specific shape is proportional to the cube of its length. That is, capacity = y = k x^3, where x stands for length.

If a box of length 30 centimeters has a storage capacity of 50 liters, then what is the specific power function that represents the capacity of a box as a function of its length?

What length would therefore be required to obtain a storage capacity of 100 liters?

What would be the storage capacity of a box of length 100 centimeters?

How long would a box have to be in order to store all the water in a swimming pool which contains 450 metric tons of water? A metric ton contains 1000 liters of water.

2. A cleaning service has been contracted to scrub the surface of the Statute of Liberty with a toothbrush. In order to estimate the time required, they use an accurate scale model on which the width of a certain finger is .8 centimeter, compared with the 20-centimeter width of that finger on the actual statute. It is found that this statue can be adequately scrubbed in .74 hours.

It is expected that the time required will be proportional to the square of the scale of the figure, as represented by the finger width.

What is the resulting power function model [time required = y = k x^2] for the time required vs. x = finger width?

According to your model, how long will it take to scrub the actual statute?

Due to the accurately of their modeling process, the company is able to complete the job on schedule. As a result they obtain contracts for scrubbing models of the Statute of Liberty across the country. How long will it take them to scrub statues whose figure widths are 2 cm, 5 cm and 7 cm?

3. The illumination of a certain light source is expected to be inversely proportional to the square of the distance from the source. That is, the illumination is a p = -2 power function.

If the illumination at a distance of 30 meters from the source is 5 foot-candles, then find the power function that models illumination vs. distance.

[For your information, a foot-candle is the illumination provided by a fairly typical candle at a distance of a foot from the flame. During the recent prolonged power outage many of us had the experience of reading with illuminations in the neighborhood of 1 foot-candle; we found that it was possible to read with this illumination, but most of us wanted quite a bit more.]

Determine the range of distances over which illumination will be within a reading comfort range of 10 - 1000 foot candles.

Cubes

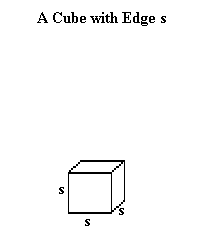
Imagine a cube. Recall that every edge of a cube has the same length, all edges meet at right angles, and a cube has 6 square faces.

Now imagine a cubical balloon as it inflates. The lengths of its edges all increase equally so that it can retain its cubical shape. The areas of its six square faces also all increase equally, and of course its volume increases.

Suppose that the lengths of the edges all double. How does this affect the area of a face of the cube? And how does this affect the volume of the cube?

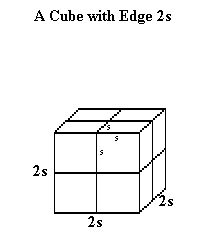
Suppose you have a pile of 1 x 1 x 1 cubic blocks, i.e., blocks whose edges all measure 1 unit. Now imagine building a 2 x 2 x 2 cube from these blocks. How many blocks will be required?

Try to answer this question before you continue reading. If necessary get out some cubes (sugar cubes aren't really cubes but they are close enough to give you the idea) and try to build a 2 x 2 x 2 cube.

You might well have concluded that to build a 2 x 2 x 2 cube you have to first build a row of two 1 x 1 x 1 cubes. However this doesn't constitute a 2 x 2 x 2 cube, since the row will be is 2 units long but only 1 unit wide and 1 unit high. If you add another similar row, you will have a layer which is 2 units long and 2 units wide, but it is still only 1 unit high. This layer clearly has 4 cubes. To build your 2 x 2 x 2 cube you need a second layer with 4 more cubes. So you need 8 cubes.

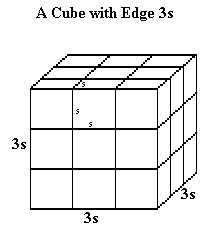
Next, before reading further, reason out how many 1 x 1 x 1 cubes will be required to build a solid 3 x 3 x 3 cube. Then reason out how many will be required for a 4 x 4 x 4 cube.

Now look at the series of cubes below. You will see a 1 x 1 x 1 cube, a 2 x 2 x 2 cube, a 3 x 3 x 3 cube and a 4 x 4 x 4 cube. Try to visualize a row of cubes along an edge, a layer consisting of identical rows, and the large cube consisting of identical layers.

You see that a 4 x 4 x 4 cube, for example, consists of 4 layers, each consisting of 4 rows with 4 cubes in each row. This gives a total of 16 cubes in each layer (four rows of four per layer), with 4 x 16 = 64 smaller cubes in the larger cube.

How many squares does it take to make a face of the 2 x 2 x 2 cube? How many does it take to make a face of each of the other two larger cubes?

4. Determine the number of cubes required to build a solid cube with an edge of 5 units. Repeat for 6, 7, 8, 9 and 10 units.

Plot the number of cubes required vs. the length of an edge.

What is the volume of a cube n units on a side?

What is the volume y of a cube which is x units on a side?

5. If every 1-unit cube (i.e., every 1 x 1 x 1 cube) weighs 35 pounds (fairly typical for wood blocks 1 foot on a side), then how much would a 3-unit cube (i.e., a 3 x 3 x 3 cube) weigh?

Does a 3-unit cube weigh more or less than 3 times a 1-unit cube? Why is this?

If the weight of a cube is a power p=3 function of the form y = k x ^ 3, then use the data point (x,y) for the 3-unit cube, where x = edge length and y = weight, to determine the value of k. Then use the resulting function to determine the weights of cubes with edge length 1, 2, 4 and 5. Do your results make sense?

6. Determine the number of 1-unit squares required to cover a 5-unit square. Determine the number of 1-unit squares required to cover 6-, 7-, 8-, 9- and 10-unit squares.

How many 1-unit squares are required to cover an n-unit square?

What is the number y of 1-unit squares required to cover an x-unit square?

Sketch a graph of the number of 1-unit squares required to cover squares of different edge lengths.

7. Suppose that it requires 4 minutes to clean each face of a 1-unit cube. How long should it take to clean a face of a 7-unit cube?

If the time required per face to clean the surface of a cube is a power p=2 function of the form y = k x ^ 2, then use the data point (x,y) for the 7-unit cube, where x = edge length and y = time to clean a face, to determine the value of k. Then use the resulting function to determine the times required to clean a single face of cubes with edge lengths 1, 2, 4 and 5. Do your results make sense?

Geometric similarity and Scale Factors

Two objects are geometrically similar if one can be obtained from the other by either stretching or compressing it by the same proportion in all directions. Geometrically similar objects have identical shapes, but may have different sizes.

A more precise definition of geometric similarity requires that every dimension of one object have a corresponding dimension on the other, and that the ratio of these dimensions always be the same.

For example consider the cones make by your sand piles. Each pile had a diameter and an altitude. If the piles were geometrically similar, then if one pile was twice as high as another it would have to have quite the diameter of the other. In this case we would say that the ratio of diameters is 2 to 1, or 2/1, or simply 2. If we found that the diameter ratio of two cone-shaped piles was, say, 1.4, while the altitude ratio was 1.7, the two cones would not be geometrically similar.

In order to understand what happens to volume as the smaller object is 'inflated' to the scale of the other, it is helpful to imagine that the smaller object is made up of a large number of tiny cubes. For example, think of a sand pile made of tiny grains of sand. The grains have a variety of shapes and sizes, and they don't pack together tightly. The shapes of individual grains aren't really very noticeable when we look at the pile. It would of course be possible to build a sand pile using cubical grains of sand, stacking layer upon layer of tightly packed cubes, building each layer of tightly packed rows, in order to mimic the shape of any given sand pile (or any other object, as far as that goes). The sides would end up in a stair-step pattern, but the steps would be no more noticeable than the irregularity of the grains in a real sand pile. You would have to look very closely to even notice the pattern.

The figure below depicts a side view of such a cone:

In order to increase the size of a pile, we could think of inflating the tiny cubes. For example to increase the dimensions of a pile by a factor of 1.3, we would simply inflate all the tiny cubes so that the edges would become 1.3 times as long. This would have the effect of increasing the diameter by a factor of 1.3 and the altitude by the same factor, thus preserving geometric similarity.

The figure below depicts the previously shown cone with the tiny cubes inflated:

This way of thinking applies to any real object. We can think of it as made up of a regular array of tiny cubes, row by row and layer by layer. We can inflate this object into a geometrically similar object by inflating the cubes uniformly in all directions.

If we increase the edges of the imaginary cubes by a certain factor, then every dimension of the object will increase by the same factor. This factor is called the scale factor. We speak of increasing the scale of the object by the scale factor. If we for example increase the scale of an object by 3, this means that the scale factor is 3, and that the sides of the cubes are increased by a factor of 3. (As you have seen, this would increase the volume of the cubes by a factor of 27).

If two objects are geometrically similar, then as one object is 'inflated' to the scale of the other, the tiny cubes of which it is constructed will inflate by the same proportion.

For example, if the scale of an object is doubled, the edge size of the tiny cubes will double. As seen before, this will increase the volume of each cube by a factor of 8. Since the number of cubes doesn't change, it is clear that the total volume of the object will increase by the same factor, 8.

8. Relating volume ratio to ratio of edges.

What is the ratio (call it volRatio) of the volume of a cube with an edge of 5 units to the volume of a cube with an edge of 3 units? What is the ratio of edge lengths? If edgeRatio stands for the ratio of edges, then what is edgeRatio^3?

What is volRatio for a pair of cubes with edges of 12.7 units and 2.3 units (the ratio is [second volume] / [first volume])? If edgeRatio stands for the ratio of edges, then what is edgeRatio^3?

What is volRatio for a pair of cubes with edges of x1 units and x2 units? If edgeRatio stands for the ratio of edges, then what is edgeRatio^3?

In general, for two cubes, how is volRatio related to edgeRatio?

9. Relating y and x ratios for a cubic proportionality.

Suppose that y = f(x) = a x^3.

We first wish to compare the y values corresponding to x1 = 3 and x2 = 5.

What is the y value corresponding to x = 3? Call this value y1.

What is the y value corresponding to x = 5? Call this value y2.

What is the ratio y2 / y1 of these y values, and what is the corresponding ratio of x values?

How do these ratios compare to those found in the first part of the preceding problem?

We next move toward a symbolic representation of this situation.

The preceding set of calculations could have been phrased as follows:

If x1 = 3 and x2 = 5, then if y1 = f(x1) and y2 = f(x2). Find y1 and y2, and determine the ratio y2 / y1 (give a numerical ratio)? How could this ratio be found from the ratio x2 / x1?

Now let x1 = 2.3 and x2 = 12.7, so that y1 = f(x1) and y2 = f(x2). Find the numerical ratios x2 / x1 and y2 / y1 and compare it with x2 / x1. How could the ratio y2 / y1 have been found from the ratio x2 / x1?

Now we represent the ratio y2 / y1 symbolically:

Let x1 and x2 represent two x values.

What are the symbolic expressions, in terms of the symbols x1 and x2, for y1 = f(x1) and y2 = f(x2)?

What then is the symbolic expression for y2 / y1?

How does this expression tell you how to find the ratio of y values from the ratio of x values?

10. Generalizing to y = x^p.

If we have the power p = 2 function y = f(x) = x ^ -2, then we can perform an analysis similar to that of the preceding problem:

If x1 = 3 and x2 = 5, then if y1 = f(x1) and y2 = f(x2). Find y1 and y2, and determine the ratio y2 / y1 (give a numerical ratio)? How could this ratio be found from the ratio x2 / x1?

Let x1 and x2 represent two x values.

What are the symbolic expressions, in terms of the symbols x1 and x2, for y1 = f(x1) and y2 = f(x2)?

What then is the symbolic expression for y2 / y1?

How does this expression tell you how to find the ratio of y values from the ratio of x values?

You have shown that for the p = 3 power function, y2 / y1 = (x2 / x1) ^3, while for the p = 2 power function y2 / y1 = (x2 / x1) ^ 2.

What do you conjecture you will get for y2 / y1 for the p = 4 power function? What would you get for the p = -2 power function? What would you get for the power p function y = a x ^ p?

Now go through the details of representing y2 / y1 for the general power function y = a x ^ p:

Suppose that y = f(x) = a x^p. Let x1 and x2 represent two x values.

What are the symbolic expressions, in terms of the symbols x1 and x2, for y1 = f(x1) and y2 = f(x2)?

What then is the symbolic expression for y2 / y1?

How does this expression tell you how to find the ratio of y values from the ratio of x values?

The figure below shows a circle stretched uniformly (i.e., by the same amount) in two mutually perpendicular directions (i.e., in the x and y directions). The circle is stretched by a factor of approximately 2 in each direction.

Every square is therefore stretched by the same amount in both directions. Every square doubles in width and in length.

At the top of the picture are three patches, one from the large circle. Directly above it and directly to its left are two patches from the small circle. It is clear from a visual inspection that the squares of the large circle are approximately twice as high and twice as wide as those of the smaller. It is also clear that one square of the large circle would be just about covered by four squares of the smaller. All these observations indicate that the squares of the larger circle have four times the area of those in the smaller circle.

The larger circle is just an inflated version of the smaller, with an identical number of squares. Since the larger circle has the same number of squares, each with four times the area, it has four times the area of the smaller.

The next figure shows a circle stretched uniformly by a factor c in both directions. Since each square of the large circle is c times as wide and c times as high as a square of the smaller circle, it has c * c = c^2 times the area. Since both circles contain the same number of squares, the area of the larger circle is c^2 times that of the smaller.

We see that the ratio y2 / y1 of areas is the square of the ratio x2 / x1 of the scale factors.

if it can be covered with squares then when inflated its proportionality is that of squares

a volume can't be so covered; a surface can; a line can't; a fractal can't

the proportionality of squares is described by y = f(x) = a x^2 or by y2 / y1 = f(x2) / f(x1) = (x2 / x1)^2

If a 3-dimensional object expands or contracts uniformly in all three directions (x, y and z), then its volume has the form V = k x^3, where x is the measure of any linear dimension of the object (e.g., x could be a diameter, a diagonal, a circumference, or anything that might be measured in feet, miles, centimeters, meters, etc.). Any quantity y which is proportional to volume (e.g., weight) will also be of form y = k x^3, though k will usually have a different value than for V.

In the case of a y = k x^3 proportionality, y2 / y1 = (x2 / x1) ^ 3.

If a 3-dimensional object expands or contracts uniformly in three mutually perpendicular directions, then any surface of the object which can be 'tiled' by tiny squares will have an area of the form A = k x^2, where x is the measure of any linear dimension of the object.

If a 2-dimensional object expands or contracts uniformly in both of the mutually perpendicular directions that can be defined on the plane, then the area of the object will have form A = k x^2, where x is the measure of any linear dimension of the object.

In either case, any quantity y which is proportional to area (e.g., time required to clean, paint required to cover) will also be of form y = k x^2.

In the case of a y = k x^2 proportionality, y2 / y1 = (x2 / x1) ^ 2.

Tiling a Sphere; Implications for Surface Area Proportionalities

** Note the above is a top view of a sphere tiles with approximately square tiles.

Exercises

scale areas, volumes

things spread out over areas, volumes

vol ratio given diameter ratio, etc.