Forces
Submit all results in the manner established for previous experiments.
Using a balance constructed from pieces of shelf standard, balanced on a knife edge
and with a brass damping cylinder partially submerged in water, we investigate the
rotational displacement of the balance from equilibrium in response to the addition of
small weights. We then use the balance with the mass set to precisely measure the masses
of various objects. See video clip on CD EPS01.
You have been supplied with a mass set and a crude
but effective and precise balance. With this balance you can with reasonable accuracy
determine the mass of an object by placing it on one side of the balance and adding masses
from the mass set to achieve a balance. The balance is very sensitive to small changes in
mass, capable of detecting changes on the order of .01 grams.
The mass set consists of masses of .1 gram, .2
gram, .3 grams, .5 gram, 1 gram, 2 grams, 3 grams, 5 grams, 10 grams, 20 grams, 30 grams,
50 grams and 100 grams. Using various combinations of these masses you can obtain any mass
from .1 gram to over 200 grams, in increments of .1 gram. Each mass is accurate to within
+-.5%.
- Note that 1 gram is, within very narrow limits of
precision, the mass of a 1 cm cube of liquid water at 20 degrees Celsius.
Place the balance beam on the stand, balanced on
the edge of the dulled blade, with the damping cylinder partially immersed in water.
- Be sure that the beam is resting as precisely as
possible at the vertex of the angle formed at the notch near its center, as demonstrated
on the video clip.
- Place a cup of water beneath the damping cylinder,
with the water depth adjusted so that the cylinder will be about halfway immersed when the
beam is horizontal.
- As shown on the video clip, adjust the position of
the washer on the beam until the damping cylinder is about halfway immersed in the water
and the beam is horizontal. Mark the position of the washer or accurately measure it from
the nearest end of the beam so that in case it moves, it will be easy to reposition. Use a
small amount of thin tape to help hold the washer in its place.
- Place a ruler or other measuring device (the
pendulum stand might be convenient for this purpose) at the position of the damping
cylinder, and note the position of the top of the beam relative to this measuring device.
Add enough water to the cup to increase the water
level by approximately 1 cm.
- What happens to the position of the beam?
- Can you explain why the position of the beam
changes, why it changes in the direction it does (i.e., up or down), and why the change is
equal to, greater than or less than the change in the water level (as the case may be)?
Now we will observe what happens to the position of
the beam when various masses are added to the balance at the position of the damping
cylinder, and also when the same masses are added at a position opposite to the position
of the damping cylinder.
- Place the .1 gram mass on the beam, at the position
of the damping cylinder. By how much does the reading on the measuring device change? By
how much would you expect the reading to change for a .2 gram mass?
- Record the mass added and the position of the beam,
as determined by the measuring device.
- Record also the position of the beam in the absence
of the added weight.
- Remove the .1 gram mass, note the reading on the
measuring device, and add the .2 gram mass.
- How much displacement corresponds to the addition of
the .2 gram mass?
- Record the mass added and the position of the beam,
as determined by the measuring device.
- Repeat twice more, first with the .3 gram and then
with the .5 gram mass.
- Now, place the .1, .2, .3 and .5 grams masses, in
turn, on the opposite side of the balance at the same distance from the balancing point as
the damping cylinder. For each mass, record the reading on the measuring device.
The position of the beam in the absence of any
added mass will be called the equilibrium position of the system. We will
construct a graph to determine the displacement of the beam as a function of the mass
added at the position of the cylinder.
- You have recorded the position of the beam at
equilibrium and with the addition of 4 masses at the position of the damping cylinder and
4 masses at the position opposite that of the damping cylinder. Place these data in a
table.
- For each line of your table, calculate the
displacement of the beam from its equilibrium position. The displacement will be either
positive or negative, depending on whether the reading on the measuring device is greater
or less than the reading at equilibrium.
- Sketch a graph of y = beam displacement from
equilibrium vs. x = added mass.
- If the graph appears to be linear, sketch the
straight line corresponding to the behavior of the system. If the graph does not appear
linear, sketch a smooth curve to fit the data as closely as possible without attempting to
go through any point except the origin (i.e., don't go out of your way to actually 'hit'
any point; come as close as possible on the average to the points you have graphed without
making nonsensical wobbles to accomodate experimental errors which have nothing to do with
the behavior of the actual system).
- Using your graph, estimate the beam displacement
corresponding to the addition of .15 gram, .25 gram, .4 gram and .7 gram at the position
of the cylinder, and opposite to the position of the cylinder.
- Place these masses on the beam at the appropriate
points and record beam positions. Compare with your predictions.
Now you will use the balance to accurately
determine the masses of various objects.
Hang the 'balance pans' at opposite ends of the
beam, at equal distances from the balancing point.
- To check the symmetry of your pan placements, take
two of the largest washers supplied with the lab kit and place one at the center of each
pan. See if the equilibrium position of the system changes, and if so how much. Then
exchange the washers between the pans and again note any change in the equilibrium
position of the system. How do your results determine whether the pans were positioned
symmetrically about the balancing point?
- If necessary, adjust the positions of the pans until
you can verify symmetry by the preceding procedure.
- With the pans unloaded, record the position of the
beam with respect to the measuring device. This will be the equilibrium position for the
balance pans.
Measure the masses of various objects.
- Place a pencil or pen in one pan, and in the other
place a combination of masses from the mass set to bring the system back as near as
possible to its equilibrium position. Add all masses in such a way that the balance pans
continue to hang symmetrically about a vertical line.
- Note the total of the masses added from the mass
set. If the balance pans have been placed at equal distances from the equilibrium
position, and if they have been kept symmetric about a vertical line, then the total of
these masses will be equal to the mass of the pencil or pen.
- Repeat this procedure to measure as accurately as
possible the mass of each washer supplied with the lab kit (if there are more than 3 of a
given type of washer, randomly select 3 washers of that type). Record these masses for
future reference.
- Determine the mass of your friction car, and record
this mass for future reference.
- Determine the masses of four randomly selected paper
clips and record these masses for future reference.
Answer the following questions:
- Why is it essential that the balancing pans be
placed at equal distances from the balancing point?
- How much would the result of weighing a 40 gram
object be affected if one pan was positioned 29 cm from the balancing point, and the other
28 cm from this point?
- If when determining the mass of a small washer, the
beam position could be brought to within .1 cm of its original position by a balancing
mass of 1.21 grams, then what might be the mass of the washer?
- Why does the beam not balance at its equilibrium
position when unequal masses are added at the two ends?
- Why does the beam not balance at its equilibrium
position when equal masses are added at unequal distances from the balancing point?
Experiment
8. Acceleration of a constant mass vs. net applied force gives a linear graph which can be
extrapolated to obtain the acceleration of gravity.
Using weights suspended over pulleys we observe the acceleration due to different
net forces on the mass of the friction car. A graph of acceleration vs. net force can be
extrapolated to a force equal to the weight of the car. Since it is this force which
accelerates the car in free fall, this extrapolated acceleration will be the acceleration
of gravity.. See video clip on CD EPS01.
As shown in the video clip,
we will relate the net force accelerating a constant mass to the acceleration of the mass.
- We will do this for two systems. The first consists
of a friction car on a level surface and a number of washers, different numbers of which
will be suspended over a pulley so that the gravitational force on the suspended washers
might provide an various accelerating forces.
- The second consists of a number of washers, with
various numbers of the washers suspended over one side of a pulley and the remainder over
the other side so that the difference results in various net gravitational forces and
hence in different accelerations of the system.
We first obtain the data necessary to determine the
acceleration of the system vs. the number of suspended washers.
- We begin with approximately 20 small washers in the
friction car. One by one we remove washers from the car and suspend them over the pulley,
continuing until the car begins to accelerate as a result of the gravitational force on
the suspended washers.
- We will use the pendulum as our timer,
synchronizeing the motion of the pendulum with the motion of the car.
- Determine the time required for the system to
accelerate from rest through a known distance under the influence of this gravitational
force. Record the pendulum length, the number of quarter-cycles, the distance traveled by
the car and the number of suspended washers.
- Add two washers and repeat, allowing the car to
accelerate from rest through the same distance.
- Continue adding two washers at a time and repeating
the process.
We determine the acceleration of the system for
each number of suspended washers.
- From the pendulum length and number of
quarter-cycles, determine the time necessary to accelerate from rest.
- From the time to accelerate from rest and the
distance, determine the average velocity, final velocity and acceleration of the system
for each number of suspended washers.
Next, plot the acceleration of the system vs. the
number of suspended washers and interpret the results.
- Plot an accurate graph of acceleration vs. number of
suspended washers and determine how well a straight line can be made to fit the data.
- Explain why the x intercept of this graph can be
interpreted as the number of washers necessary to overcome the frictional resistance of
the system.
- Create another table for the acceleration of the
system vs. the number of suspended washers, but this time subtract the number of washers
that corresponds to the x intercept of the graph from the number of suspended washers.
Call the resulting quantity the net number of accelerating washers.
- Plot acceleration vs. the net number of accelerating
washers.
- Assuming that gravity exerts the same force on each
suspended washer, how well do your results confirm Newton's Second Law, which states that
the acceleration of a system of constant mass is directly proportional to the net force on
the system?
- Describe another experiment that would be necessary
to completely validate Newton's Second Law.
- The frictional characteristics of the pulley and
that of the wheels of the friction car are approximately, but not exactly, the same.
Assuming that the ideal graph, which results when the frictional characteristics of the
pulley and the wheels of the car are the same, is perfectly linear, then how might the
differing frictional characteristics affect the linearity of the graph as more and more
washers are suspended over the pulley (which results in a greater influence by the
frictional characteristics of the pulley and a lesser influence by those characteristics
of the car).
Use your results to predict the acceleration of the
entire system when the net force is equal to that of the gravitational force on the mass
of the system:
- Using the shelf-standard balance and the weight set,
determine the mass of a single washer and of the friction car (or, if these quantities
have already been determine, simply list the results).
- How many washers would be required to equal the mass
of the entire system? According to your graph of acceleration vs. net number
of accelerating washers, what acceleration would be expected if the system was subjected
to the force of gravity on this number of washers?
- If the system is simply dropped and allowed to fall
freely to the floor, it will accelerate in response to the force exerted by gravity on its
mass. What will this acceleration be?
Repeat this experiment using weights suspended over
a pulley (an Atwood Machine):
- Suspend 30 paper clips and two large washers over a
pulley, with 15 clips and a single washer on each side, as indicated on the video clip.
- One at a time, transfer paper clips from one side to
the other, until the system begins accelerating when released.
- Measure the distance the system falls from rest and
the time required. Spin the pulley and repeat twice more, for a total of three
measurements with the pulley in a different initial position for each.
- Transfer another paper clip and repeat.
- Continue until the time of fall is less than 1.5
seconds.
- Calculate accelerations and graph acceleration vs.
force. Force is measured in units of paper clip weights; each transfer of a paper
clip results in an increase in net force of 2 paper clip weights (the weight a paper clip
is added to one side and removed from the other, resulting in a force difference equal to
two paper clip weights).
- The x intercept of your graph corresponds to
frictional force. For each data point, subtract frictional force from total force to
get net force and plot acceleration vs. net force.
- Determine from your graph whether, within
experimental uncertainties, acceleration is proportional to net force (i.e., if the graph
of acceleration vs. net force is a straight line through the origin).
- Determine the mass of a paper clip and of a large
washer, using the shelf standard balance.
- Use your graph to show that the acceleration of the
system is in the same proportion to the acceleration of gravity as the difference of the
masses on the two sides to the total mass of the system, when the difference of the masses
is corrected for friction.
Experiment
9. The force tending to pull a pendulum back toward its equilibrium position is in the
same proportion to the weight of the pendulum as the displacement from equilibrium to the
length of the pendulum..
See video clip on CD EPS01.
By displacing a pendulum with various numbers of equal masses suspended over a
pulley, we determine the nature of the relationship between the displacing force and the
displacement of the pendulum.
In this experiment we suspend
a spherical pendulum bob of known mass by a string of known length to form a simple
pendulum. We then displace the pendulum by means of various known masses suspended over a
pulley to establish the relationship between pendulum displacement and suspended mass.
- Begin by suspending the large concrete sphere, the
mass of which is indicated on the sphere, by means of a string of length at least one
meter. Measure and record the length of the pendulum from the center of the sphere to its
fixed point of attachment.
- As shown in the video clip, set up the pulley and a
measuring device, with the measuring device located so as to measure the relative position
of the string at a point just above the pendulum bob. Note and record the length of the
string from its fixed point of attachment to the point at which its position is to be
measured.
- Attach a thread to the tab at the side of the
pendulum bob, with the other end of the thread running over the pulley and with a hook at
the end of the string over the pulley. Note the position of the pendulum string as
indicated by the measuring device. This position will be taken as the equilibrium position
for the system.
- To the hook suspended over the pulley, attach a
20-gram weight and record the position of the string.
- Increase the mass suspended from the pulley to 40
grams and record the position of the string.
- Repeat with masses of 60, 80 and 100 grams.
- Create a table for position measurement vs.
suspended mass, and add a column for the displacement from equilibrium.
- Construct an accurate graph of y = pendulum
displacement from equilibrium vs. x = suspended mass. Fit a straight line to this graph.
- Your graph should, within experimental
uncertainties, give you a straight line through the origin. Use the slope of this graph to
estimate the displacement from equilibrium corresponding to a suspended mass of 150 grams,
and to a suspended mass of 200 grams. From these estimates, predict the position of the
pendulum due to each suspended mass.
- Suspend masses of 150 grams and 200 grams from the
pulley and see if your predictions are correct.
Now check out the proportionalities involving
forces and distances.
- The force exerted on the pendulum bob by the tension
in the thread is in fact somewhat less than the force exerted on the suspended mass by
gravity. This is due to the friction associated with the pulley. This friction reduces the
force by approximately 4%, so that the actual force exerted on the pendulum will be
approximately .96 of the force exerted by gravity on the suspended weight. Thus the
effective suspended masses can be regarded as .96 of the actual suspended masses.
- Make a table of pendulum displacement from
equilibrium vs. effective suspended masses.
- Based on this table, create another table of [
pendulum displacement / length of string to measurement position ] vs. [ effective
suspended mass / mass of pendululm bob ].
- If we let x = pendulum displacement at measurement
position, L = length of pendulum string to measurement position, m = effective suspended
mass and M = mass of pendulum bob, then this last table shows (x / L) vs. (m / M).
- Does your table, within experimental uncertainty,
confirm the hypothesis that pendulum displacement as a proportion of pendulum string
length (i.e., x/L) is identical to the ratio of masses (m / M)?
- Construct a graph of effective suspended mass m vs.
pendulum displacement x. Fit a straight line to your graph and determine its slope `dm /
`dx.
- If it is in fact true that x / L = m / M, then x / m
= L / M so that the slope `dx / `dm must be equal to the unchanging ratio L / M.
- How well do your results confirm the hypothesis that
x / L = m / M?
Use the proportionality x / L = m / M to predict
various displacement and suspended masses.
- Use the proportionality to predict the displacement
x corresponding to a suspended mass of 70 grams. Recall that m stands for the effective
suspended mass, which for this pulley with its 4% coefficient of friction is .96 of the
actual suspended mass.
- Hang a 70 gram mass from the hook and see how well
the observed displacement corresponds with your prediction.
- Use the proportionality to predict the effective
mass m that will lead to a displacement of 2.3 cm from the equilibrium position.
- Hang the appropriate mass (i.e., one whose effective
mass is equal to that you predicted) from the hook and see how well the observed
displacement corresponds to the desired 2.3 cm displacement.
Justify the following statements:
- Since the weight of an object is equal to the force
exerted on it by gravity, which is proportional to mass, then if F is the force of gravity
on the effective mass and W the weight of the pendulum bob, m / M = F / W and therefore x
/ L = F / W. That is, the displacement is in the same proportion to the length of
the pendulum as the applied force to the weight of the pendulum.
- If a force F is applied to the pendulum in the
horizontal direction, then the displacement of the pendulum from equilibrium will be F / W
times the length of the pendulum.
- The length and displacements of the pendulum as
measured in this experiment were not the actual length and actual displacements of the
pendulum. The actual length should have been measured to the center of the sphere,
and the displacements should have been measured at this position. However, the
ratios x / L obtained in the experiment are identical to the x / L ratios that would have
been obtained had these quentities been measured at the center of the sphere.
Analysis of Errors
- Estimate the errors in your effective masses and in
your measurements of pendulum position, and represent your errors on the appropriate
graph.
- Discuss the implications of your errors.
Note that the results obtained here are
only valid as long as the displacement of the pendulum from equilibrium is small compared
to its length.
- If displacement is less that .1 of the length, then
predictions of forces or displacements are accurate to within +-.5%, or +-.005 of the
actual quantities.
Experiment
10. Rubber bands can be calibrated to measure force with reasonable accuracy.
Click here for Physics 121 Short Version
By pulling back a pendulum of known length and mass using two attached strings with
a rubber band between them, we see that the additional force required to pull the pendulum
back further and further results in a greater and greater stretch of the rubber band. By
measuring the length of the rubber band vs. the displacement of the pendulum we infer and
graph force vs. stretch for the rubber band. Repeating the experiment with two identical
rubber bands in series, then again with the two rubber bands in parallel, we compare the
forces exerted by these combinations with the force of a single rubber band. We store our
calibration of the rubber bands in a convenient calibration program. We repeat this
experiment for two different types of rubber bands.. See video clip on CD EPS01.
We can measure forces using a rubber band and a
scale by which to measure the stretch of the rubber band. The force vs. stretch curve is
not linear for a rubber band. For a spring which is light compared to its strength, a
force vs. stretch curve would be very nearly linear; however we choose here to use the
rubber band in part because it is readily available and cheap, and in part for the very
reason that it is nonlinear, and is nonlinear to a degree that forces us to account for
it.
We begin by using the rubber band to
displace a simple pendulum of known mass and length through a variety of displacements.
- Using the largest pendulum bob, construct a pendulum
whose length is at least 1 meter, and set up a measuring device by which to measure the
displacement of the pendulum. Record the length of the pendulum to the point of
measurement, and ulcer record the equilibrium position of the pendulum.
- Take two pieces of thin string,
each about 50 cm long, and tie a hook to each end of each piece. You can use small paper
clips to make the hooks.
- You have two kinds of rubber
bands. Hook one of the thinner rubber bands and the two pieces of string together, with
the rubber band between the strings.
- Attach one end of the string to
the tab on the surface of the pendulum bob, using the hook at that end of the string.
- Pull the string straight
back, keeping it horizontal, until the rubber band just begins to stretch. Place something
on the free end of the string so that the system remains stationary and measure the length
of the rubber band.
- Pull back a bit further, until the
rubber band looks like it has stretched about half a cm beyond its original length. Note
the position of the pendulum and the length of the rubber band.
- Continue pulling back, stopping each time the end of
the rubber band looks like it has stretched another half a cm, and at each position record the length of the rubber band
and the position of the pendulum.
- Stop when the pendulum displacement exceeds 10% of
its length, or when the rubber band has reached more than 1/3 of its length (if you
stretch it beyond that length it will probably get permanently stretched and have to be
recalibrated).
- When you have finished, construct a table of rubber
band length vs. pendulum position. Add a column for rubber band stretch and one for force.
- In the column for rubber band stretch, fill in the
magnitude of the stretch of the rubber band in excess of its length when it begins to
stretch.
- In the column for force, determine the magnitude of
the force corresponding to the appropriate pendulum displacement. (The weight of the
pendulum is equal to the force exerted on it by gravity, which is W = m g; this weight
will be in Newtons when m is in kg and g in m/s^2. The pendulum mass in grams should be
marked on the pendulum. If it is not you may assume a mass of 1100 grams.).
We sketch a graph of force vs. rubber band
stretch.
- Construct an accurate graph of force, in Newtons,
vs. rubber band stretch, in meters.
- Submit a description of this graph, and speculate on
the reasons for its shape.
- Keep your graph for future reference.
Repeat the experiment for two rubber bands hooked 'in parallel' (i.e., both
stretched between the same two hooks). Repeat all steps except the parts
using the parallel and series combinations.
- Based on your observations and your graphs, how does the force exerted by two identical
rubber bands 'in parallel' compare to that exerted by one?
- Why do you think it should be so?
Repeat the experiment for two rubber bands hooked 'in series' (i.e., one
attached to the end of the other, like a chain; you might make a second hook for this
purpose). Repeat all steps except the parts using the parallel and series
combinations.
- Based on your observations and your graphs, how does the force exerted by to identical
rubber bands 'in series' compare to that exerted by a single rubber band?
- Why do you think it should be so?
We proceed to calibrate the single rubber
band.
- Using the program CALIBRT (download from the homepage if
necessary; run by clicking on the name of the program in Explorer), enter your data and
store your calibration.
- The program CALIBRT is designed to calibrate any
measuring device. We use it here for rubber bands.
- The program will ask you for the zero-point
reading. This is the reading just before the rubber band began to stretch, when the
force (the 'quantity your are measuring') is essentially zero.
- The zero-point reading may vary the next time you
insert a rubber band into the apparatus; the program that later converts your data
according to the calibrations will compensate for this variation by asking you for your
zero-point reading everytime you use it.
- You then enter the remaining points, according to
instructions.
- When you name your calibration file, you should
write down the name of the file and the type of rubber band you calibrated.
We calibrate another rubber band by hanging
weights.
- As described on the video clip, suspend the thin
rubber band next to a vertical scale (e.g., the pendulum stand).
- Hang masses of 5, 25, 50, 75, 100, 125, 150, 175 and
200 grams from the rubber band (but do not let the stretch exceed 1/3 the length of the
rubber band) and record the positions of the end of the rubber band.
- Make a table of force in Newtons vs. stretch in
meters.
- Construct a graph of force vs. stretch.
- Compare the shape of this graph with that obtained
for the thickest rubber band.
- Run the CALIBRT program and save your calibration of
this rubber band.
Using the same procedure, calibrate this rubber
band. Be sure to mark the rubber bands for future use.
The CALIBRT program also reads your previos
calibration file and converts new data to the appropriate units.
- Calibrt creates a table under the filename you give
it, which you can open and cut-and-paste into your document.
- Calibrt also creates a comma-delimited text file
under the same filename but with an .XCL extension, of your data which can be opened in a
spreadsheet.
- Calibrt creates one more file, under the filename
with an MTH extension, which can be imported into DERIVE.
- All these files will be in your C:\CALIB724 directory.
Answer the following questions:
- According to the CALIBRT program, what force would
be associated with each rubber band, given the following displacements: 1.2 cm, 1.9
cm, 2.6 cm, 3.3 cm, 4.8 cm, 6.6 cm, 8.2 cm and 10.3 cm?
- How well do the values given by the CALIBRT program
agree with those you would estimate from your graph?
Analyze the errors in this experiment.
Calibrating Rubber Bands: Physics 121 Short
Version
If a rubber band is not stretched to a length more than 30% greater than its
unstretched length, and if it is not left in a stretched position for a long time, it will
usually not experience any sort of permanent stretch. We can thus calibrate a rubber band
by using it to suspend known mass, and plotting the mass or weight of the supported mass
vs. the length of the rubber band.
Calibrate the thinnest rubber band:
- First measure the maximum unstretched length of the rubber band--the length when the
'slack' is gone but no significant tension yet exists.
- Using a thin rubber band suspended at top by a hook made from a paper clip, hang weights
of 10, 25, 50, 75, ... grams from another hook at the bottom of the rubber band. For each
mass accurately measure the length of the rubber band.
- For each length determine the stretch of the rubber band -- i.e., its length in excess
of its maximum unstretched length.
- Sketch a graph of suspended mass or weight vs. rubber band stretch.
- Fit a smooth curve to your grap
h (a sample graph is shown below).
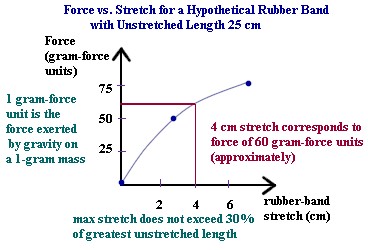
- Use this curve to estimate the suspended mass or weight that would be required to
support 20, 40 and 60 and 80-gram masses.
- Keep your graph for reference in future experiments.
Calibrate two of the thin rubber bands connected in series (i.e., connected to
form a chain).
- First connect the two rubber bands using a paper clip.
- The paper clip will not stretch during the experiment, so the stretch you measure will
be just the total stretch of the two rubber bands.
- Repeat the procedure of the first calibration.
Calibrate two of the thin rubber bands connected in parallel (i.e.,
both stretched between the same two hooks).
- Repeat the procedure of the preceding calibrations, except use masses of 10, 50, 100,
150, ... grams..
Predict the calibration graph for three rubber bands in series, then test your
results.
- Sketch a predicted calibration graph for three rubber bands in series.
- Using the same masses as for the two rubber bands in series, obtain data and sketch the
corresponding graph.
Calibrate two of the thicker rubber bands connected in series.
- Using masses of 10, 100, 200, 300, ... grams, obtain the data necessary to construct a
calibration graph for two of the thicker rubber bands connected in series.
- Construct a graph and retain for future reference.
Based on the graphs you have, construct the graphs you would predict for each
of the following:
- A single of the thicker rubber bands.
- Two of the thicker rubber bands connected in parallel.
- 10 of the thin rubber bands connected in series.
- 10 of the thin rubber bands connected in parallel.
- 10 of the thicker rubber bands connected in series.
- 10 of the thicker rubber bands connected in parallel.
How accurate do you think your predictions are?
Experiment
11. For any given angle, the weight of an object is completely equivalent to the resultant
of two mutually perpendicular forces with one at the given angle from vertical.
By suspending various masses from two perpendicular strings with inserted rubber
bands, we can determine the force exerted by each string. By changing the angles of the
two strings while maintaining the right angle between them, we infer at different angles
the components of the weight vector for the suspended mass, and compare our results with
the predictions of vector analysis. (see video clip on CD EPS
01).
In this experiment we suspend a weight from two
mutually perpendicular strings, neither in the vertical or the horizontal direction. We
measure the tension forces in the strings by means of force balances with calibrated
rubber bands, and infer the components of the weight in a coordinate system defined by the
strings.
First set up the experiment and obtain data.
- First determine the size of the rubber bands to be
used. They must be strong enough to support a 200-gram mass, while still stretching enough
to give useful stretch measurements, but not stretching by more than 1/3 their original
length. If necessary you can use 'double' rubber bands (i.e., two rubber bands in
parallel), being sure to take account of the doubling in your calculations of force.
- Suspend a known mass of approximately 200 grams from
two force balances, as shown in the video clip.
- Adjust the directions of the strings until one makes
an angle of approximately 10 degrees with horizontal (corresponding to a slope of around
.15 with horizontal) and the other is perpendicular to it. It is essential that the two
directions be as close to perpendicular as possible.
- Note the lengths of the rubber bands.
- Using a sheet of paper, make the markings you will
use to determine the actual angles of the forces exerted (see the video clip). On the
paper record the lengths of the rubber bands and the known mass.
- Repeat this process for angles near 20 degrees
(slope approx. .3), 30 degrees (slope approx. .6) and 40 degrees (slope approx. .85).
Determine the actual tensions, and the angles of
the tensions with horizontal.
- Use your graph of mass or weight vs. rubber band
stretch to determine the forces corresponding to the rubber band stretches.
- Use tan^-1 (`dy / `dx) to find the direction of each
string, as in the video clip.
For each trial, determine the angles and magnitudes
of the weight components, and show that the vector sum of the weight components is equal
in magnitude and direction to the weight of the suspended mass.
- The weight components are equal and opposite to the
two forces of tension.
- From the angles and magnitudes of the weight
components, determine the horizontal and vertical components of each.
- Determine the sum of the horizontal and vertical
components of the weight components.
- Show that, within the limits of experimental error,
the weight components are indeed equivalent to the weight vector.
Answer the following questions:
- How should this experiment and demonstration
convince you that the weight of the suspended object can be regarded as the resultant of
two components in two mutually perpendicular directions?
- How do the relative magnitudes of the two components
change as the angle of the component nearest horizontal changes from 10 degrees to 40
degrees? What would happen if the angle continued to 50, 60, 70 and 80 degrees?
- What would be the tension forces if one tension was
vertical and the other horizontal?
Analyze the errors inherent in this experiment.
Experiment
11b: The Mass or Weight of a Suspended Object can be Inferred from the Tensions in
and Angles Of the Supporting Rubber Bands
When an object is suspended from two calibrated rubber bands, with the tops of the
rubber bands attached to two pencils protruding over the edge of a tabletop, the
magnitudes of the supporting forces are inferred from the calibration graph(s), and the
directions of the supporting forces from the length of the rubber bands and the separation
of the pencils. From the magnitudes and angles of the two forces we determine the
horizontal and vertical components of these forces and compare the sum of the vertical
components with the weight or mass of the suspended object; we compare also the magnitudes
of the horizontal components of the forces.
We first suspend an appropriate mass vertically from two identical rubber-band
supports.
- Place a single thin pencil so that its end protrudes over the edge of a level tabletop.
Place a weight (a book would work well) on the other and of each pencil to keep it in
place.
- We will refer to a pair of rubber bands connected in series by a paper clip in the
middle as a 'rubber-band support'.
- Construct two rubber-band supports, using either the thicker or the thinner rubber
bands.
- Use paper-clip hooks to hang the two rubber-band supports from the end of the pencil.
- From the other ends of the two supports use paper-clip hooks to suspend a weight which
will stretch the rubber bands by approximately 10% of their original length.
Obtain data for support length vs. pencil separation
The first figure below shows the configuration of the system with lengths L of the
rubber-band supports and the separation S of the pencil ends.
- With pencil separation 0 (i.e., both weights hanging from a single pencil end), measure
the lengths L of the two rubber-band supports, from the pencil to where the hook at the
other end supports the hanging weight. Ideally these lengths will be the same or
very nearly the same (this should be the case unless the rubber bands are not identical,
which could be the case if they have been over-stretched).
- Move the pencils to separation S = 10 cm and measure the new lengths L of the
rubber-band supports. Record this information, including the separation of the pencils.
- Repeat for pencil separation of 20, 30, 40, ... cm, until one or more of the rubber-band
supports has exceeded its unstretched length by 30%.

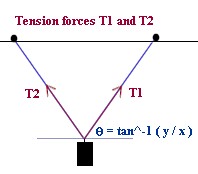
Determine tension forces and angles for the rubber-band supports
The second figure above depicts the tension forces which support the hanging mass or
weight.
- For each length of each support, use your calibration graph (similar to that shown
below) to determine the corresponding tension in the rubber band.

- Tension is the force tending to pull the rubber band back to its original length.
- If your calibration graph is in grams of supported mass vs. stretch, you may treat grams
as force units as long as you understand that a gram is really a unit of mass, not force,
and what we choose to call a gram unit of force really refers to the force exerted by
gravity on a 1-gram mass.
- Hand-sketch a reasonably accurate picture of the system for each separation.
- You need not actually measure distances to scale, but you should make a reasonable
attempt to estimate relative distances so that the angles in your sketches are reasonably
close to the actual angles of the system.
- For each sketch construct a right triangle for each rubber-band support, with the
support (including the paper clips at the ends) forming the hypotenuse and a vertical leg
extending from the hanging mass upward.
- The horizontal leg will have a length equal to half the separation of the two pencils.
Determine the length of the vertical legs using the Pythagorean Theorem.
- Determine the angle made by each support with horizontal by finding tan^-1 ( y / x ) ,
where y is the length of the vertical leg and x the length of the horizontal leg.
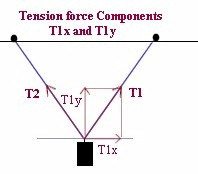
Sketch and Analyze Force Vectors

- Sketch the force vectors corresonding to the tensions and find the x and y components of
the forces.
- For each pencil separation, sketch the force vector corresponding to the right-hand
rubber-band support. The length of the vector should represent the amount of force, and
the angle should be the angle found from the preceding analysis.
- Label each vector with its angle and the magnitude of the force.
- Determine the horizontal and vertical components of each force vector, using your
knowledge that Fx = F cos(`theta) and Fy = F sin(`theta) (see figure above).
- For each separation, add up the y components of the two supporting forces, and also add
up the x components of these forces.
- Note that the x components are in different directions, so one will be negative while
the other is positive, while the y components are both in the same direction.
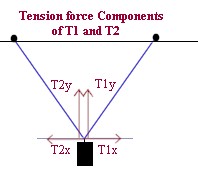
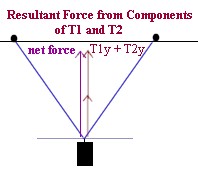
Answer questions:
- What should the x components add up to, and why?
- What should to y components at up to, and why?
Experiment
12. The net force on a friction car released on a ramp is proportional to the 'effective'
slope of the ramp, for small slopes.
For various slopes we determine the force required to prevent the friction car from
rolling down a straight, slightly vibrating incline. We also determine the slope at which
the car rolls down the incline at a constant velocity. A graph of acceleration vs.
effective slope (effective slope is slope in excess of the constant-velocity slope) tests
whether the relationship is nearly a proportionality for small slopes. See video
clip on
CD EPS01.
The 'effective' slope of a ramp is the slope in
excess of the (small) slope necessary to overcome friction -- the slope at which the
friction car moves down the ramp at a constant velocity.
By observing the displacement of a pendulum by the
net force accelerating the friction car down a ramp, we conclude that for small slopes the
net force exerted on a car coasting down a ramp is proportional to the 'effective' slope
of the ramp.
We begin by determining the slope at which the car
moves down the ramp at constant velocity.
- By changing the slope and vibrating the ramp
slightly, as demonstrated on the video clip, determine the heights of the ramps at two
ends for the slope at which the car tends to move down the ramp at constant velocity.
- Calculate the 'constant-velocity' slope.
We next determine the forces required to prevent
the car from accelerating down the ramp for various slopes in excess of the
constant-velocity slope.
- Using the light pendulum bob, set up a pendulum and
a means of measuring the displacement of the pendulum.
- Using the procedures developed in the previous
force-on-a-pendulum experiment, obtain the data that will permit you to determine the
force required to prevent the car from accelerating down the incline for various slopes.
- Use approximately 5 slopes equally distributed
between the constant-velocity slope and a slope of approximately .1.
For each slope, keep tapping the incline to
vibrate it slightly and make observations which will allow you to find the desired force.
For each slope record the data from which we will
calculate the value of the slope.
- Organize your data into a table.
We convert our data to force vs. slope information.
- From your data table, obtain the force in Newtons
and the slope corresponding to each trial.
- For each slope, subtract the constant-velocity slope
to obtain the effective slope.
- Present your force vs. effective slope data in a
table.
We now plot force vs. effective slope and interpret
the results.
- Construct an accurate graph of force in Newtons vs.
effective slope.
- Sketch the straight line that best fits the data.
- Determine whether this straight line indicates a
force vs. effective slope proportionality.
- Recall that a proportionality is indicated when,
within the limits of experimental error, the straight line passes through the origin and
the data points.
Compare the slope of the graph with the weight of
the car, and draw conclusions about accelerating forces and accelerations.
- From the mass of the car determine its weight. Is
the weight, within experimental error, equal to the slope of the graph?
- Can we as a result conclude that, for small slopes
at least, the force required to restrain the car from accelerating down the incline is
equal to the weight of the car multiplied by the effective slope of the incline?
- Can we conclude that for small slopes, the net force
accelerating a car coasting down that slope is equal to the weight of the car multiplied
by the effective slope of the incline?
- How can we therefore conclude that the acceleration
of a friction car down a small slope is equal to the acceleration of gravity multiplied by
the effective slope of the incline?
Under the assumption that a coffee filter dropped from a height on the order of one
meter reaches its terminal velocity in a negligibly short time after covering a negligibly
short distance, we compare terminal velocities of single, doubled, tripled and quadrupled
coffee filters by dropping them simultaneously from various heights and adjusting the
heights until all the filters reach the floor at the same time. We investigate the
power-function relationship between weight and terminal velocity, and the relationship
between velocity and the force of air resistance.
If it is assumed that
terminal velocity is an all cases reached in a negligibly short time, then by
simultaneously dropping a number of nested coffee filters and a single filter from
different heights so that both objects strike the floor simultaneously, we can determine
the ratio of terminal velocities. A graph of number of filters vs. velocity is easily
converted to a graph of force vs. velocity, and the nature of the proportionality between
force and velocity can be determined.
We begin by dropping a single filter and doubled
filter, as shown on the videotape.
- Two identical filters will be used. In one filter we
will place a single crumbled-up filter, effectively creating a 'doubled' filter identical
to the other except with twice the mass.
- The single filter and the doubled filter should
present the same area to air resistance as they fall. To check for possible differences,
the crumpled filter will be switched from one of the original filters to the other.
- We drop the doubled filter from a fixed height of at
least 1 meter, and preferably higher. We adjust the height from which the single filter is
dropped until, when the two filters are dropped simultaneously, they strike the floor
simultaneously.
- Having found the desired height, switch the crumpled
filter and repeat the experiment, using the same heights. If the filters still strike the
floor simultaneously, then we conclude that the difference in terminal velocities is due
only to the difference in the mass and not to the surface area exposed to air resistance.
- Since the filters take equal times to reach the
floor, the ratio of their average velocities will be the same as the ratio of the heights
from which they are dropped.
We next drop the single filter and a tripled
filter, then the single filter and a quadrupled filter.
- The procedure is identical to the one used for the
doubled filter. For the tripled filter we add two crumpled filters to a single filter.
- Again we will find the heights from which the single
filter reaches the floor in the same time is the tripled filter. And again we will switch
the crumpled filters and repeat the drop from the same heights to validate our results.
- Again the ratio of the velocities of the single and
tripled filters will be the ratio of the distances fallen.
- We repeat for a quadrupled filter, this time adding
three crumpled filters to a single filter.
We make a table and graph for force vs. terminal
velocity.
- Let w0 stand for the weight of the single filter.
Then the weights of the doubled, tripled and quadrupled filters will be 2 w0, 3 w0 and 4
w0.
- Let v0 stand for the average velocity of the single
filter and express the velocities of the doubled, tripled and quadrupled filters as
multiples of v0. For example, if the doubled filter is found to travel at 1.6 times the
average velocity of the single filter, then its velocity will be expressed as 1.6 v0.
- Make a table for weight vs. average velocity. Then
sketch a graph of the table.
- Explain the following: Since at terminal velocity
the air resistance on the filter is equal to its weight, and since we assume that terminal
velocity is obtained very quickly so that the average velocity of a falling filter is very
close to its terminal velocity, our table of weight vs. average velocity will constitute a
table of air resistance vs. velocity.
Attempt to linearize the data using a
power-function transformation of the velocity.
- Attempt to linearize the table by either squaring
(taking the 2d power) or taking the square root (taking the .5 power) of the average
velocity, whichever results in the more nearly linear graph.
- Test to see whether a nearby power (e.g., the 1.8 or
the 2.2 power if the 2d power more nearly linearized the data; the .4 or .6 power if the
.5 power did a better job) does a better job of linearizing the data.
Determine the power-function relationship between
terminal velocity and force.
- If we let F stand for force and vTerm for terminal
velocity, then if p is the power of the transformation of vTerm required to linearize the
data, it follows that F is proportional to vTerm ^ (1/p).
- What power of vTerm do you conclude is proportional
to the force F of air resistance?
Answer the following:
- Why do we expect that the results will be more
accurate when the filters are dropped from greater heights?
- How could you design and experiment to observe the
effect of the non-negligible time required for a single filter to reach terminal velocity
on the average velocity at different heights?
Using the shelf standard balance with the damping cylinder partially immersed, we
compare the force required to offset a specific change in the water level on the cylinder.
We determine the change in the immersed volume of the cylinder and compare the mass of an
equivalent amount of water with the offsetting force.
Here we test Archimedes'
Principle, which tells us that the buoyant force on a submerged object is equal to the
weight of water displaced by the object. We then use this principle to determine the
mass densities of a variety of objects.
Set up the shelf-standard balance in a horizontal
configuration with water reaching a marked point on the damping cylinder.
- On the damping cylinder place two marks, one about
1.5 cm below a point halfway between the bottom in the top of the cylinder, and another 3
cm above the first.
- Place a cup beneath the balance so that it is
possible to fill the cup and cover either mark.
- By adjusting the water depth and the position of the
washer on the balance, put the system in a configuration where the beam of the balance is
horizontal and water reaches the lower of the two marks.
Add weights and add water to achieve a horizontal
configuration with water reaching a higher marked point on the damping cylinder.
- Now using your mass set, add weights to the beam at
the position of the damping cylinder and add water to the cup until the beam is again
horizontal and the water level reaches the second mark on the cylinder.
- Note the total mass added, and from this total mass
determine the weight that was added at the position of the cylinder.
Determine the weight of the displaced water and
compare with the weight added at the position of the cylinder.
- The damping cylinder has a diameter of .25 inch.
From this information determine the additional volume of the water displaced when the
additional 3 cm of the cylinder was immersed.
- At 1 gram / cm^3, what mass of water was displaced
by the additional 3 cm of the cylinder? What is the weight of the displaced water?
- How does the weight of the displaced water compare
with the weight of the masses that were added at the position of the cylinder?
Answer the following questions:
- What evidence does this experiment give us that when
an additional length of the cylinder is immersed, there is an upward buoyant force exerted
on it?
- To what extent do your results support the
hypothesis that, when the additional 3 cm of the cylinder were immersed, an upward buoyant
force was exerted on the cylinder which was equal to the weight of the additional water
displaced?
- Why was it important to have the beam horizontal for
both of the measurements made in this experiment?
We now determine the weight of a bolt and its
apparent weight when immersed in water, from which we infer the buoyant force on the bolt
and the density of the bolt.
- Carefully unscrew one of the bolts embedded in the
blue Styrofoam disk in your kit. Tie a thread around the bolt and suspend it from one end
of the beam on your shelf-standard balance. By adding masses at an equal distance on the
other side of the balance, determine the mass of the bolt and infer its weight.
- Position a cup of water so that the bolt is immersed
in the water. Find the mass necessary to balance the bolt when it is subject to the
buoyant force of the water, and infer its apparent weight in water.
- From the actual weight and the apparent weight of
the bolt, determine the buoyant force on the bolt.
- This buoyant force is equal to the weight of the
water displaced. What is the ratio between the weight of the bolt and the weight of the
water it displaces?
- What therefore is the mass density of the bolt, in
grams / cm^3?
Repeat this experiment with various household
objects, determining the mass density of each.
- In your own words, describe how this procedure works
to give us the mass density of an object.
Devise an experiment of your own, using the same
apparatus with procedures similar to those used above, to show that when an object floats,
the buoyant force on the object is equal to the weight of the object.







