Short Lab Kit Experiments for Physics I

Note that these experiments are demonstrated on the CD labeled EPS02

Conservation of Momentum

This experiment has been modified. See Experiment 19 (Revised) for the modified instructions.

Using the two large balls:

From the horizontal distance traveled by the ball when it leaves the ramp without interference and the vertical distance of fall determine its velocity at the end of the ramp (from vertical distance of fall you can determine the time required to fall, which you combine with the horizontal distance to get the horizontal velocity).
From the same information for the second ball after collision its after collision velocity.
Determine whether momentum is conserved in the collision.

Using the large and small balls (small ball as target):

From the horizontal distance traveled by the ball when it leaves the ramp without interference and the vertical distance of fall determine its velocity at the end of the ramp (from vertical distance of fall you can determine the time required to fall, which you combine with the horizontal distance to get the horizontal velocity).
From the same information for each of the balls after collision determine their velocities after collision.
From momentum conservation determine the mass ratio m2 / m1 of the balls.
You may see the writeup for Experiment 19 for more detail on how to calculate some of these quantities.

Rotation of Beam

Associated video clip is on the CD EPS02 under Short Lab Kit Experiments.

IMPORTANT NOTE: See Modified Rotation Beam Instructions and Setup. Compared to the clip, you will be substituting the metal strap for the wooden 'beam', and you should balance the strap on the.die ('die' is the singular of 'dice') that came with your kit rather than the cap of a Mr. Sketch Marker.

To improve stability and increase the moment of inertia, you should use the two ceramic magnets that also came with your kit; attach them near the ends of the strap and position the strap with the magnets underneath the strap rather than on top of it (the system will be much more stable with the magnets underneath the strap).. This is depicted in the figure shown with the Modified Rotation Beam Instructions and Setup .
It is important that the die be level; otherwise the metal strap will rotate off the die and you won’t be able to get your data. If you have too much trouble with the strap rotating off the die you can reduce its initial velocity by angling the end of the parperclip so that it slips off sooner.
You will accelerate the system using a 'chain' of rubber bands, as directed in the Modified Rotation Beam Instructions and Setup .

Modified Rotation Beam Instructions and Setup (this is from Rotation Beam experiment; not part of Velocity of a Pendulum experiment)

Setup

For this experiment you will use the metal strap, the die ('die' is sigular of 'dice'; you should have one in your kit) and the two ceramic magnets from your kit.

The first of the two figures below shows a side view of the metal strap balanced on the die ('die' being singular of 'dice'), with the two ceramic magnets on the underside of the strap, near the ends of the strap.

The second figure is a top view of the strap as it would appear if the strap was clear, with the die and the magnets visible beneath. In this view the system is free to rotate in the clockwise or counterclockwise direction.

Figure 1: Side view of setup.

Figure 2: Top view of setup. The strap will rotate clockwise or counterclockwise.

Overview of Actvity

The system will be set up on a table. Place a sheet of paper on the tabletop, the die on top of the paper and the strap (with magnets and paperclips) on top of the tie.

You are going to give the system a nudge so it rotates about the die, and you are going to see how far it 'coasts' after you nudge it, and how long it takes to come to rest.

Start with the system as shown in the figure below, orientated left-to-right. Somehow mark the right end of the strap so you can keep track of that end (mark it with a pencil or a pen, put a little sticker on it, or something like that)..
Make a line segment on the paper, parallel to the strap, from about the center of the strap toward the end you have marked, as indicated in the first of the two pictures in the figure below.
Give the system a push with one finger so that it rotates in the counterclockwise direction, while you use the other hand to click on either a stopwatch or the computer timer used in previous experiments. Determine the time required for the system to come to rest; if the end you marked passes its original position, count a complete revolution for every time it does so.
When the system comes to rest make another line segment on your paper, as indicated, starting near the center and extending in the direction of the marked end of the strap. This segment will make an angle with your first segment, as shown in the second picture.

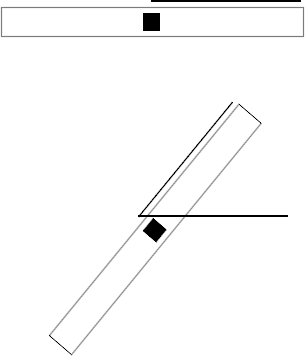
Measure the angle between the two lines segments marked on your paper.

Note also the number of complete revolutions made by the strap, recalling that 1 complete revolution is 2 pi radians.

From the number of complete revolutions, the angle you measured and the direction of rotation, determine the angle in radians through which the strap has rotated.

For example, for the figure above, assuming that the angle is 50 degrees.

If the strap in the above figure rotated in the clockwise direction, and if the mark on the strap never passed its original position, then the strap is 50 degrees short of a complete revolution. This indicates a rotation of 360 deg - 50 deg = 310 degrees, which is 310 * pi rad / (180 deg) = 31 pi / 18 radians, or about 5.4 radians. (To be completely accurate we would note that a clockwise rotation is negative, couterclockwise is positive, so this angle would really be -31 pi / 18 radian, or about -5.4 radians).
Had the strap rotated to this position in the counterclockwise direction, without the mark passing the original point, the angle would be just 50 degrees, or nearly .9 radian.
Suppose that the strap rotated to this position by rotating counterclockwise, and had completed one full revolution before coming to this position. Then its rotation would be 1 revolution + 31 pi / 18 radians, or 2 pi + 31 pi / 18 radians, which comes to approximately 11.7 radians. We could get the same result by saying that the rotation is 360 deg + 310 deg = 670 deg; multiplying 670 deg by pi rad / (180 deg) we would again 67 / 18 pi rad, which simplifies to about 11.7 rad. Noting the counterclockwise direction of rotation we would regard this as -11.7 rad.
If the rotation had been counterclockwise, and if two complete revolutions had already been completed, then the angle might be calculated as 360 deg + 50 deg = 410 deg, which would then convert to about 7.2 rad.

Take your data

Give the system a nudge sufficient to keep it coasting for at least 4 seconds, and in the manner described above determine the angle through which it rotates.

Using the angle and the time required, determine the average angular velocity of the system in radians / second.

Assuming that the angular velocity changes at a constant rate, determine the initial angular velocity. Use the same reasoning you used earlier with objects accelerating from rest on an incline, except that this time the final angular velocity is zero. So you are answering the question: If angular acceleration is uniform, final angular velocity is zero and average angular velocity is as you calculated it, then what is must be the initial angular velocity?

Repeat this process for three more trials. You will obtain different time intervals and different angles of rotation.

Show your data and your analysis.

Answer the following questions

How consistent are the angular accelerations?

Why is it that the system slows down and eventually comes to rest?

Does the angular acceleration appear to be related in any systematic way to the average angular velocity of the system?

******** The instructions below do not apply to this version of the experiment. *********************************

Set up as instructed on video clips.

Be sure that the thread from the pendulum remains close to perpendicular to the beam until it slips off.

Obtain your data:

Mark initial position, final position and position at which the thread slips off the beam.
Note pendulum displacement at beginning at at the position where the thread slips off the beam.
Use a timer to find the time required for each phase of the motion, from start until the string slips off, then from the time the string slips off until the system comes to rest.

Find angular velocities and accelerations:

From the angular distance (i.e. the angle between start and the release of the thread) and time required for the washer-pendulum to accelerate the system determine the average and final angular velocities for this phase of motion, and the angular acceleration.
From the angular distance and time required from the release of the thread to rest determine the average and final angular velocities and the angular acceleration for this phase of motion.

Analyze your motion and force data:

Assuming acceleration to be uniform, how should the average angular velocities compare? Do they compare as would be predicted?
From the length and mass of the pendulum (30 grams for a washer of diameter a little over 5 cm, 16 grams for the 4.5 cm diameter) and its average displacement from equilibrium determine the average force exerted on the beam (recall that the force is in the same proportion to the pendulum weight as displacement from equilibrium to the length of the pendulum).

Analyze the relationships among torque, moment of inertia and angular acceleration:

Determine the torque on the system (use the force you just obtained and the distance from the axis of rotation to the point of application of the force near the end of the beam).
Assuming that the moment of inertia of the system is .001 kg m^2, use Newton's Second Law for rotation (torque = moment of inertia * angular acceleration) to determine the average angular acceleration expected of the system. Compare to the acceleration you obtained for the first phase of motion.
Assuming that friction is what stops the system, the acceleration observed in the second phase of motion should be the result of the torque exerted by friction. Use Newton's Second Law for rotation, with this acceleration and the moment of inertia given above, to find this torque.
Subtract this torque from the torque exerted by the pendulum to get the net torque on the system, and calculate the acceleration that should result from this torque. Compare to the acceleration you obtained for the first phase of motion.

Velocity of a Pendulum

Associated video clip is on the CD EPS02 under Short Lab Kit Experiments.

Pull a pendulum with a small disk resting on it (a small washer or a penny works fine) of length at least 1.5 meters back 10 cm, 20 cm, 30 cm and 40 cm and, as shown in the video clip, stop it abruptly at its equilibrium position for each distance. Determine for each distance how far the small disk falls and how far it travels horizontally.

Use the SHM program (download from Sup Study ... > Course Documents > Downloads > Physics I) to match the horizontal motion of the pendulum with that of the vertical line in the simulation. Note the angular velocity of the point on the reference circle. Instructions for using this simulation are at revised_instructions_for_SHM_program.htm .

Analyze your Data:

For each pullback distance the motion of the pendulum should be modeled by a circle whose radius is equal to the pullback distance. Be sure you understand why.
As the pendulum passes the equilibrium position the point on the circle is moving in the horizontal direction, so the velocity of that point should equal the velocity of the pendulum. For each radius, determine the velocity of the point on the circle (you can use the definition of the radian along with the angular velocity, or you can use the fact that there are 2 `pi radians in a revolution to determine the time required for a revolution, which with the circumference of the circle allows you to calculate the velocity).
How should the horizontal velocity of the projectile with the velocity of the point on the circle compare?
How do they compare?