Problem: An object with mass 6.9 kilograms is initially at rest. What will be its velocity after being acted upon by a net force of 58.65 Newtons for 8.5 seconds? How far will it travel during the 8.5 seconds? What kinetic energy will it attain?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The acceleration of a 6.9 Kg object under the influence of a 58.65 Newton force will be a=F/m=( 58.65 Newtons)/( 6.9 Kg)= 8.5 meters per second per second. In 8.5 seconds the velocity will be 8.5( 8.5) = 72.25 meters per second. The average velocity will be the average of this velocity and zero, or ( 72.25 + 0)/2 meters per second = 36.12 meters per second. At this average velocity, in 8.5 seconds the object will move 307.0 meters. The kinetic energy will be KE = .5( 6.9 Kg)( 72.25 m/s)^2 = 18000 Joules.
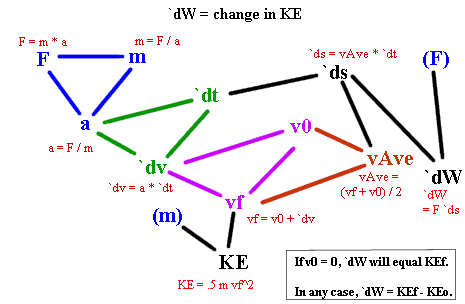
Generalized Response: If an object of mass m, initially at rest, is acted upon by a net force F for time interval `dt, it will experience acceleration a = F / m for time interval `dt. This will result in a velocity change `dv = a `dt = F / m * `dt. Since the object started from rest its final velocity will be
vf = 0 + `dv = F / m * `dt
and its average velocity will be
vAve = (v0 + vf ) / 2 = (0 + F / m * `dt) / 2 = (1/2) (F / m) `dt.
The distance traveled by the object will be
`ds = vAve `dt = (1/2) (F / m) `dt * `dt = (1/2) (F / m) * `dt^2.
The kinetic energy attained by the object will be
KE = .5 m vf^2 = .5 m (F / m * `dt) ^ 2 = (1/2) F^2 / m * `dt^2.
.
.
.
.
.
.
.
.
.
.
Figure description: The figure below shows the complete relationship between the work done by the net force and the kinetic energy gained by the object. For the purposes of this problem, note that vf is obtained by the same series of relationships as before and ignore everything to the right of v0. Note that if we simply combine our knowledge of vf with the originally given mass m, we obtain KE = .5 m vf^2. As determined earlier, if v0 = 0 then vf = F / m * `dt, so after a little substitution and simplification we will find that KE = (1/2) F^2 / m * `dt^2.
