Problem: An object with mass 9.9 kilograms is initially at rest. What will be its velocity after being acted upon by a net force of 89.1 Newtons for 9.1 seconds? How far will it travel during the 9.1 seconds? How much work is done?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The acceleration of a 9.9 Kg object under the influence of a 89.1 Newton force will be a=F/m=( 89.1 Newtons)/( 9.9 Kg)= 9 meters per second per second. In 9.1 seconds the velocity will be 9.1( 9) = 81.9 meters per second. The average velocity will be the average of this velocity and zero, or ( 81.9 + 0)/2 meters per second = 40.95 meters per second. At this average velocity, in 9.1 seconds the object will move 372.6 meters. The work done will be the product of the distance 372.6 m and the 9.9 Newton force, or 33190 Joules.
Generalized Response: If an object of mass m, initially at rest, is acted upon by a net force F for time interval `dt, it will experience acceleration a = F / m for time interval `dt. This will result in a velocity change `dv = a `dt = F / m * `dt. Since the object started from rest its final velocity will be
vf = 0 + `dv = F / m * `dt
and its average velocity will be
vAve = (v0 + vf ) / 2 = (0 + F / m * `dt) / 2 = (1/2) (F / m) `dt.
The distance traveled by the object will be
`ds = vAve `dt = (1/2) (F / m) `dt * `dt = (1/2) (F / m) * `dt^2.
The work done on the object will be
`dW = F `ds = F (1/2) (F / m) * `dt^2 = (1/2) F^2 / m * `dt^2.
.
.
.
.
.
.
.
.
.
.
Explanation in terms of Figure(s), Extension
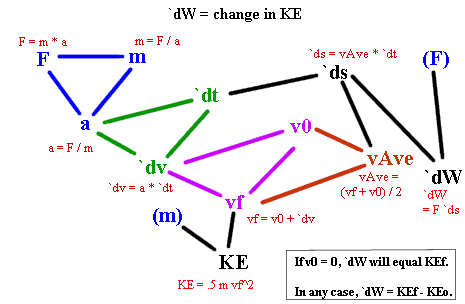
Figure description: The figure below shows the complete relationship between the work done by the net force and the kinetic energy gained by the object. If we find `ds as done in previous problems, we can then combine this result with the known force F to obtain the work `dW.As determined earlier, if v0 = 0 then `ds = (1/2) (F / m) * `dt^2. After a little substitution and simplification we will find that `dW = F `ds = (1/2) F^2 / m * `dt^2.
Figure(s)
