Problem: If an object of mass m is acted on by a net force F, it will increase in velocity at the rate a=F/m, where a is in meters per second per second when F is in Newtons and m in kilograms (a is called the acceleration of the object). This is Newton's Second Law. Remember it, and remember its name. An object of mass 7 Kg is acted on by a net force of 26 Newtons. By how many meters per second per second does the object's velocity change? By how many meters per second will its velocity increase in 6 seconds?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The first question is asking for the rate at which velocity increases, which is a=F/m=( 26 Newtons)/( 7 Kg)= 3.714 meters per second per second. Changing by 3.714 meters per second every second, in 6 seconds the increase will be ( 6 sec)( 3.714 m/sec/sec) = 22.28 m/s. Since the object started from rest, this will also be its velocity after 6 seconds.
Generalized Response: The rate at which velocity changes, or the acceleration, is a = F / m. During a time interval `dt, the velocity will therefore change by a `dv = (F / m) `dt. If the object starts from rest its final velocity will therefore be 0 + `dv = (F / m) `dt.
.
.
.
.
.
.
.
.
.
.
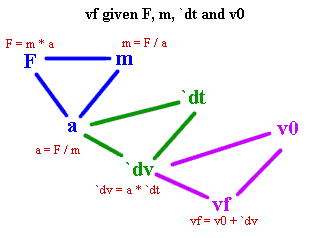
Figure description: The first figure below depicts a 'flow' triangle for an object of mass m subjected to a force F. The relationship a = F / m can be understood as saying that greater force implies proportionally greater acceleration for a given mass while greater mass implies proportionally less acceleration for a given force. The relationship F = m * a can be understood as saying that to achieve a given acceleration a greater force must be exerted on a greater mass and that for a given mass a greater acceleration will require a greater force. The relationship m = F / a tells us that for a given observed acceleration the greater the force the greater the mass being accelerated, and for a given applied force a greater acceleration implies that less mass is being accelerated.
The second figure depicts a 'flow' diagram for an object of mass m, initially with velocity v0, subjected to a force F for time interval `dt. From the force and the mass we deduce the acceleration (the 'blue' triangle). From the acceleration and the time interval we deduce the change `dv in velocity (the 'green' triangle). From the change in velocity and initial velocity we obtain the final velocity (the 'purple' triangle).