Problem: The kinetic energy of an object can be shown to be .5mv^2, where m is its mass and v its velocity. When mass is in Kg and velocity is in m/s, kinetic energy will be in Joules. What is the kinetic energy of a 14 Kg object moving at 4 m/s? What is its kinetic energy at double this speed? When speed doubles, by what factor does kinetic energy increase?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: When v is 4 m/s and m is 14 Kg, ||value missing for ke|| = .5( 14Kg)( 4m/s)^2 = .5( 14Kg)( 4m/s)^2 = 112 Joules. The same procedure, using ||value missing for doubleV|| m/s, yields kinetic energy 448 Joules. The factor by which the kinetic energy increases is the ratio 448/ 112 = 4 of these results.
Generalized Response: At velocity v, the kinetic energy of a mass m is KE1 = .5 m v^2. At velocity v' = 2v, the kinetic energy is
KE2 = .5 m (v')^2 = .5 m (2v) ^ 2 = .5 m (4 v^2).
The ratio of kinetic energies is therefore
KE2 / KE1 = .5 m (4 v^2) / (.5 m v^2) = 4.
More generally if velocity increases by factor c, from v to v' = cv, the kinetic energy will increase from KE1 = .5 m v^2 to KE2 = .5 m (cv)^2 = .5 m (c^2 v^2), and the ratio of kinetic energies will be KE2 / KE1 = c^2. Kinetic energy increases by the square of the velocity increase. As seen above doubling velocity doubles kinetic energy. If velocity is tripled kinetic energy will increase by factor 3^2 = 9. If velocity increases to 10 times its original value kinetic energy will increase by factor 100. This, incidentally, is the reason why it is so much worse to run your car into a solid object at 60 mph than at 30 mph: the KE is four times as great at 60 mph than at 30 mph. It also takes 4 times as far to stop a car from 60 mph than from 30 mph.
.
.
.
.
.
.
.
.
.
.
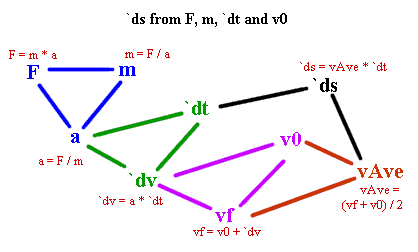
Figure description: The figure below depicts a 'flow' diagram for an object of mass m, initially with velocity v0, subjected to a force F for time interval `dt. From the force and the mass we deduce the acceleration (the 'blue' triangle). From the acceleration and the time interval we deduce the change `dv in velocity (the 'green' triangle). From the change in velocity and initial velocity we obtain the final velocity (the 'purple' triangle). From initial and final velocities we obtain average velocity (the 'red' triangle) and from average velocity and `dt we obtain the displacement `ds.
