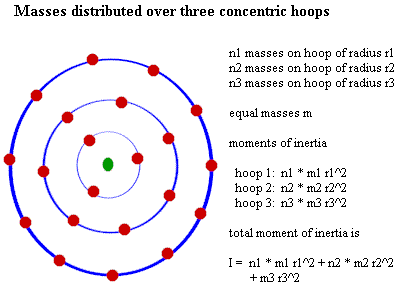
Problem: A series of 3 concentric massless hoops are constrained to rotate together about an axis through their common center and perpendicular to their common plane. The first hoop has radius 11.9 meters, the second a radius of 23.8 meters and the third a radius of 35.7 meters.
Masses of 10 kilograms are attached to each hoop, with masses separated by `pi / 3.966 meters of arc length along the circumference of each hoop.
If a torque of 1256 meter Newtons is applied, what will be the angular acceleration?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The first circle or hoop has a total circumference of 2 `pi ( 11.9 meters). With masses spaced at `pi / 3.966 meters, the number of masses on the first circle or hoop will be
number of masses on first hoop = 2 `pi ( 11.9 meters)/( `pi / 3.966 meters) = 2( 11.9)( 3.966) = 94.39.
Noting that the second and third circles or hoops have double and triple the circumference of the first, with masses spaced identically to the first, there will be 2( 94.39) and 3( 94.39) masses on the second third circles or hoops.
At 10 kilograms per mass, the circles or hoops will have respective masses
hoop masses = 943.9 kilograms, 1887 kilograms, and 2831 kilograms.
The moments of inertia of the circles or hoops are thus
hoop 1: ( 943.9 kg)( 11.9 meters) ^ 2 = 1.123 * 10 ^ 4 kg m ^ 2,
hoop 2: ( 1887 kg)( 23.8 meters) ^ 2 = 2.245 * 10 ^ 4 kg m ^ 2, and
hoop 3: ( 2831 kg)( 35.7 meters) ^ 2 = 3.368 * 10 ^ 4 kg m ^ 2.
The total moment of inertia is therefore the sum of these mr ^ 2 contributions, or 6.736 * 10 ^ 4 kg m ^ 2.
A torque of 1256 meter Newtons will result in an acceleration of
`alpha = `tau / I = 1256 meter Newtons / 6.736 * 10 ^ 4 kg m ^ 2 = .01864 rad/second ^ 2.
.
.
.
.
.
.
.
.
.
.
Figure Description: The figure below depicts masses distributed uniformly over three concentric hoops. The moment of inertia of a hoop of radius r containing n masses, each of mass m, will be I = (hoop mass) * r^2 = n * m r^2. The total moment of inertia will be the total of the moments for the individual hoops