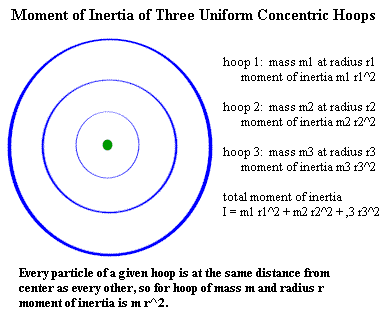
Problem: A series three concentric hoops are constrained to rotate together about an axis through their common center and perpendicular to their common plane. The first hoop has radius 9.4 meters, the second a radius of 18.8 meters and the third a radius of 28.2 meters. Each hoop has a mass density of 5.984 kilograms/meter. Find the angular acceleration of the system if a torque of 1974 meter Newtons is applied.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The first circle or hoop has circumference 2 `pi ( 9.4 meters) = 59.03 meters. Its mass is therefore 59.03 meters ( 5.984 kilograms/meter) = 353.2 kg.
The second circle or hoop has circumference 2 `pi ( 18.8 meters) = 118.0 meters. Its mass is therefore 118.0 meters ( 5.984 kilograms/meter) = 706.1 kg.
The third circle or hoop has circumference 2 `pi ( 28.2 meters) = 177.0 meters. Its mass is therefore 177.0 meters ( 5.984 kilograms/meter) = 1059 kg.
The three moments of inertia will therefore be
hoop 1: ( 353.2 kilograms)( 9.4 meters) ^ 2 = 9.357 * 10 ^ 4 kg m ^ 2,
hoop 2: ( 706.1 kilograms)( 18.8 meters) ^ 2 = 2.495 * 10 ^ 5 kg m ^ 2, and
hoop 3: ( 1059 kilograms)( 28.2 meters) ^ 2 = 2.808 * 10 ^ 5 kg m ^ 2.
These add up to the total moment of inertia 6.238 * 10 ^ 5 kg m ^ 2. The 1974 meter Newton torque will result in an angular acceleration of `alpha = `tau / I = 1974 meter Newtons/( 6.238 * 10 ^ 5 kilogram meter ^ 2) = .003164 radians/second.
Generalized Response: A hoop of radians r and mass density `lambda, measured in kg / meter, will have circumference 2 `pi r and therefore total mass
hoop mass = 2 `pi r * `lambda.
If the hoop rotates about its center, then its entire mass lies at the same distance from the axis of rotation; the entire mass moves as a unit and therefore has moment of inertia
I = m r^2 = 2 `pi r * `lambda * r^2 = 2 `pi r^3 * `lambda.
A series of hoops with radii r1, r2, ..., rn, each with the same density `lambda, will have circumferences
hoop circumferences 2 `pi r1, 2 `pi r2, ..., 2 `pi rn,
masses
hoop masses 2 `pi r1 * `lambda, 2 `pi r2 * `lambda, ..., 2 `pi rn * `lambda,
and will therefore have moments of inertia
hoop moments of inertia 2 `pi r1^3 * `lambda, 2 `pi r2^3 * `lambda, ..., 2 `pi rn^3 * `lambda.
The total moment of inertia will be
I = 2 `pi r1^3 * `lambda + 2 `pi r2^3 * `lambda + ... + 2 `pi rn^3 * `lambda = 2 `pi `lambda * ( r1^3 + r2^3 + ... + rn^3).
The acceleration resulting from applying a torque `tau will therefore be
angular acceleration = `tau / I = `tau / [ 2 `pi `lambda * ( r1^3 + r2^3 + ... + rn^3) ].
.
.
.
.
.
.
.
.
.
.
Figure Description: The figure below depicts three concentric hoops. Each hoop has its own mass and radius and therefore its own moment of inertia. The moment of inertia of the combination is the of the individual moments.