Problem: The act of displacing an object on a spring by a distance y from its equilibrium position requires work, which is recovered and changed to KE when the object is released. The work done is therefore considered to exist in the system as potential energy. Upon release, this potential energy is recovered and changed to kinetic energy until the object reaches its equilibrium position. After that, the object passes through the equilibrium position and begins exerting a force against the restoring force of the spring. It therefore does work against the spring, which is stored in the form of potential energy. This potential energy reaches its maximum at the instant the object reaches its extreme position. Then the process begins once more, with the object gaining kinetic energy at the expense of its potential energy until the kinetic energy is once more maximized at equilibrium point. If there are no dissipative losses, the process continues indefinitely.
What is the work required to move an object from equilibrium to a point 3.4 meters from equilibrium, against a restoring force governed by the constant k = 6.8 Newtons/meter? How much additional work would be required to then move the object to a point 13.1 meters from equilibrium? If the object was released from rest at this position, what then would be its kinetic energy at a point 1.7 meters from equilibrium? What would be the object's kinetic energy at its equilibrium point?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The work required to move the mass from one position to another is equal to the average force multiplied by the distance moved. For two positions on the same side of the equilibrium position, the fact that the force is a linear function of position ensures that the average force is equal to the average of the forces at the two positions.
To move from equilibrium to 3.4 meters from equilibrium, the average force is the average of the ( 6.8 Newton/meter) ( 3.4 meter) = 23.12 Newton force at this position and the force at equilibrium, which is 0. The average force is therefore 11.56 Newtons. The distance is the 3.4 meters from equilibrium to the position, so the work is
work from equilibrium to first point = ( 3.4 meters)( 11.56 Newtons) = 39.3 Joules.
This will be the potential energy at the 3.4 meter position.
Moving from the 3.4 meter position to the 13.1 meter position requires moving through a distance of ( 13.1 - 3.4) meters; the average force is the average of the 23.12 Newton force at 3.4 meters and the 13.1 meter ( 6.8 N/m) = 89.08 Newton force experienced at the 13.1 meter position. The work is thus
work from first to second point = ( 13.1 - 3.4) meters [ 89.08 Newtons + 23.12 Newtons]/2 = 544.1 Joules.
This results in a total potential energy of
PE at 13.1 meter position = 39.3 Joules + 544.1 Joules = 583.4 Joules.
{Note that the same PE would have been found by averaging the force at equilibrium and at the extreme 13.1 meter position, then multiplying by the 13.1 meters the object has been moved from equilibrium. You should verify this.}
After being released, the object moves back to the 1.7 meter position, where its potential energy is found by the previous method to be 9.826 Joules. By energy conservation, with the assumption that no energy is dissipated, the difference between the maximum 583.4 Joule potential energy and the 9.826 Joule potential energy must be present in the form of kinetic energy. This difference is 573.5 Joules. This is the kinetic energy at the 1.7 meter point.
At the equilibrium point, there is no potential energy; the original 583.4 Joules of potential energy has therefore been converted completely to kinetic energy.
Note that the total of the kinetic and potential energies at every point is 583.4 Joules. This is the potential energy at the extreme point, where the object is for an instant at rest with no kinetic energy; it is the kinetic energy at the equilibrium point, where there is no potential energy; and it is the sum of the kinetic and potential energies at the 1.7 meter point. The total energy PE + KE of the system, at any point, must be 583.4 Joules.
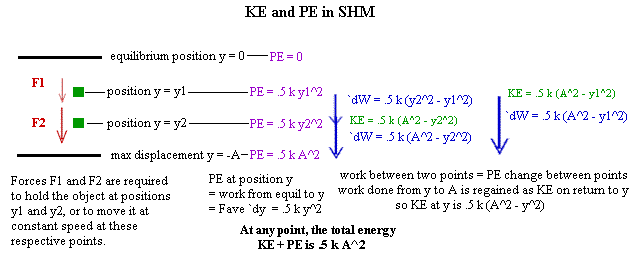
Generalized Response: The work required to move against a linear restoring force F = - k y, from equilibrium to displacement y from equilibrium is
work from equil to y = `dW = Fave `ds = [ (k * y + 0) / 2 ] * y = .5 k y^2,
where Fave is the average force that must be exerted to move the object at constant velocity at the instant its displacement is y. This work is done on the object by the restoring force as it returns from position y to the equilibrium point, as is manifested as KE. We therefore say that the PE at position y is .5 k y^2.
The PE at positions y1 and y2 is respectively PE1 = .5 k y1^2 and PE2 = .5 k y2^2; the work required to get from y1 to y2 can be derived by using the average force and distance between these points, but this is unnecessary, since by conservation of energy the work is just the PE difference
work from y1 to y2 = `dW = dPE = PE2 - PE1 = .5 k (y2^2 - y1^2).
This work is equal to the KE gained while accelerating from y2 to y1 under the influence of the restoring force.
The maximum PE will occur at the extreme point, where y = A or -A; the PE will be
PE at extreme point y = +- A: PE = .5 k A^2.
Since the PE at any point is .5 k y^2, the PE loss from an extreme point to position y is
PE loss from A to y = .5 k A^2 - .5 k y^2 = .5 k (A^2 - y^2).
This PE loss is the KE at position y.
.
.
.
.
.
.
.
.
.
.
Figure Description: The figure below shows an object at positions y1 and y2 between the equilibrium and extreme positions. The PE is shown at every indicated position, as is the work from y1 to y2, from y2 to extreme position A, and from y1 to extreme position A. The KE at y1 and at y2 is also shown; note that it is equal to the work `dW from the point to the extreme point.
