Physics II Class 01/13

indexed

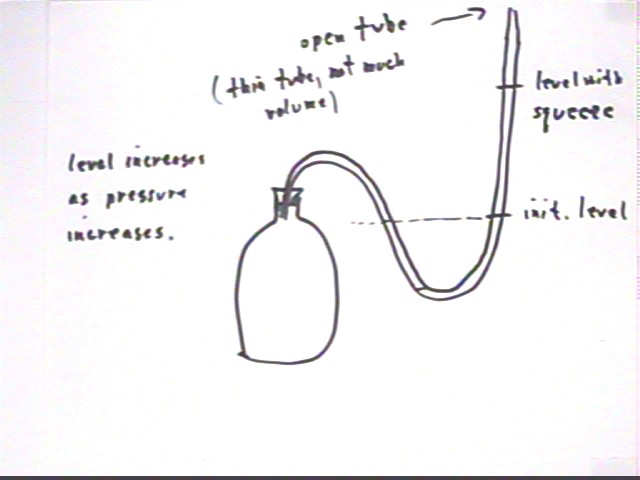
The situations observed during the preceding class are summarized below, with the figure representing a column of alcohol in a thin U tube (inner diameter 1/8 inch) partially filled with alcohol and extending from a sealed 3-liter bottle, represented by the figure below.

• When the top of the tube was open to the atmosphere a significant but modest squeeze of the bottle raised the level of the alcohol about half a meter.
• When the top of the tube was closed a hard squeeze barely changed the level of the alcohol.
• When the last half-meter of the tube was nearly level and open to the atmosphere the temperature change induced by the instructor's palm in contact with, but not squeezing, the container apparently caused the alcohol column to move a few centimeters within a minute or so.

The fluid in the tube initially had equal pressures in the 'bottle side' (point B) and the 'open side' (the vertical part of the tube, which includes point A).  The initial fluid level was the same in both sides of the tube; this initial level is not represented in the figure.  

When the bottle was squeezed a bit we found that the fluid was displaced in the counterclockwise direction so that the level in the vertical part of the tube, open to the atmosphere, is greater than that in the 'bottle side' of the tube.

We wish to compare the pressure at A with that at B.  Call these pressures PA and PB.

• The pressure in a continuous stationary fluid is the same at equal depths, so the pressure is the same at B and C.
• The pressure in a continuous stationary fluid increases with increasing depth, so the pressure increases as we move 'down' the vertical tube from point A to point B.
• We therefore conclude that the pressure at A is less than that at C, and that the pressure at C is the same as that at B.
• From this we conclude that PA < PB.

This conclusion is consistent with our intuition that by squeezing the bottle we increased the pressure of the air inside the bottle.  Note that the pressure at point B, where the air in the bottle meets the fluid in the tube, is the same for the air as for the fluid.  

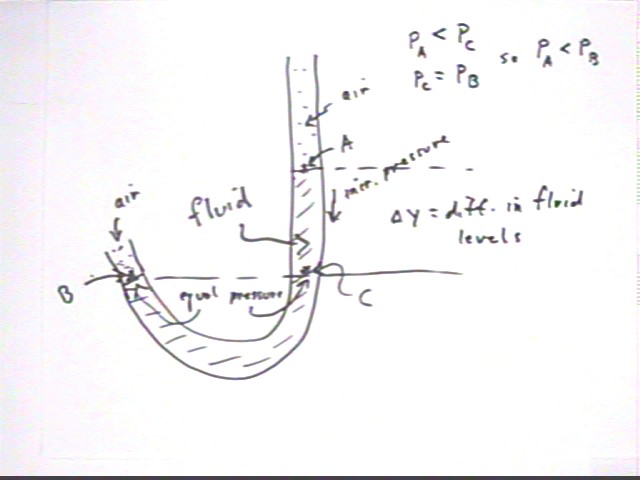
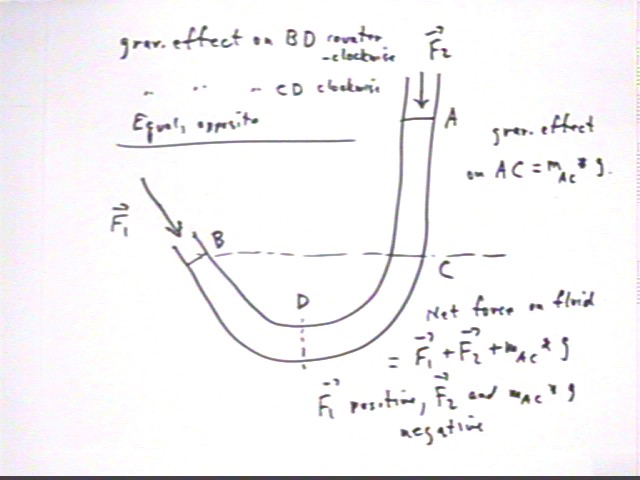
The situation can be analyzed from the point of view of Newton's Second Law.  Since the fluid is stationary we conclude that the net force on the fluid is zero.  There is a force F1 exerted on the fluid at point B, tending to accelerate the system in the counterclockwise (positive) direction, and a force F2 at point A which tends to accelerate the system in the clockwise (negative) direction.

• If F1 and F2 were the only forces involved they would have to be equal and opposite, since the fluid is stationary.
• However there are also gravitational and normal forces acting on the fluid.
• The total  gravitational and normal force acting in the segment BD is equal and opposite to the total gravitational and normal force acting on the fluid in segment CD, so the fluid in BC makes zero contribution to the net force.
• The gravitational force exerted on the fluid in segment AC is m_AC * g, where m_AC is the mass of the fluid in segment AC.  If the tube is vertical there is no normal force in this segment and we see that the net force on the fluid is F1 + F2 + mAC * g, where the boldface characters indicate vector quantities.
• Since the net force is zero, and since F1 acts in the negative direction, we conclude that - F1 + F2 + m_AC g = 0 so that F1 = F2 + m_AC g.  Note that now F1, F2 and g are not boldfaced and hence indicate the magnitudes of the quantities.
• Since F1 = F2 + m_AC g we see that F1 must be greater than F2, consistent with the idea that the pressure at point B is greater than that at point A.

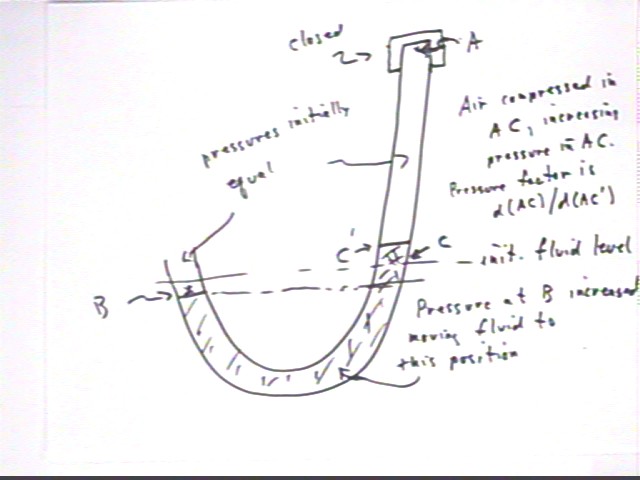
In the situation depicted below the vertical tube is closed at point A.  We consider what we observed when the bottle was squeezed with the tube closed, compared to when the tube was open.  A much harder squeeze than before resulted in only a small change in the position of the fluid.

• The change in the position of the fluid changes the fluid level from the initial level C, where the level was the same in both sides of the tube, to level C '.  This shortens the column of air originally confined to AC.
• Since the cross-sectional area of the tube is constant, the volume ratio of the vertical column of air is therefore d(AC ' ) / d(AC), where d(XY) stands for the distance between points X and Y.
• The pressure of the shorter column is therefore d(AC) / d(AC ' ) times the original pressure.

Noting that the difference in level B and level C ' is small compared to the difference observed with the open tube, and that the squeeze  necessary to create the large difference in the open tube was much less than the squeeze used to get the small difference with the closed tube, we conclude that the pressure difference between level C ' and level B is much smaller than the pressure difference due to the compression of the air in segment AC. 

The situation depicted below will demonstrate how the pressure in a stationary fluid depends only on the density of the fluid, the depth and the gravitational acceleration.

• We consider a container with uniform cross-sectional area A, filled to depth y with a fluid of density rho.  
• The volume of the fluid is A * y, so that its mass is density * volume = rho * A * y and the weight of the fluid is therefore weight = - rho A y g (implicitly using the upward direction as positive).
• Since the fluid is stationary its acceleration is zero, so the net force on the fluid is zero.  There must therefore be (an)other force(s), equal and opposite to the weight, acting on the fluid.
• This force is the normal force exerted by the base of the container on the fluid.

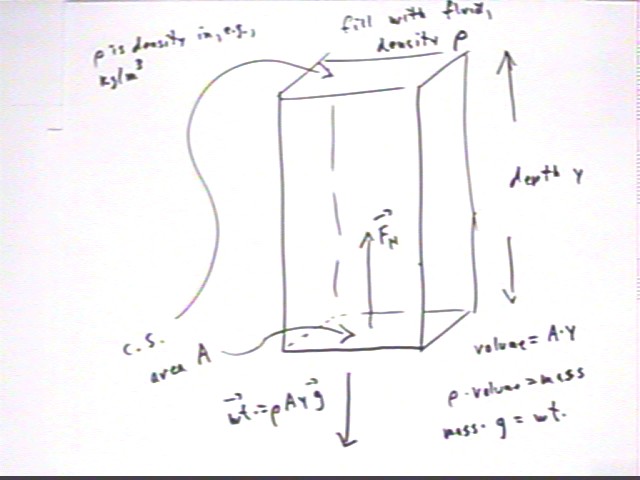
The force Fnormal is therefore 

• Fnormal = rho g A y.

This force is equally distributed over the base of the container, so it makes sense to speak of the force per unit area.

This force per unit area is the pressure.  A simple calculation shows us that at depth y the pressure is

• P = Fnormal / A = rho g A y / A = rho g y.

We now consider a container filled to depth y, relative to a hole from which fluid can exit.

The demonstration is class showed such a system (a plastic bottle with a hole poked in the side).  As water exited the hole and decreased the depth of the water, the velocity of the exiting water decreased, thereby decreasing the rate at which water exits the container.  The result is a decrease in the rate at which the depth decreases.

The pressure of the water is the source of the force which accelerates water out through the hole.

• The pressure at the upper surface of the water is atmospheric pressure, represented P_atm.
• The fluid adds pressure rho g y at the level of the hole, so that inside the container, where the water is stationary, the pressure is rho g y + P_atm.
• The pressure outside the hole is P_atm.

If the water flows thru a short tube on its way out of the container, assuming that the only forces exerted are by the pressure, then we see that the water in the tube experiences force F_c = (rho g y + P_atm) * A to the right and force F_b = P_atm * A to the left.  (This model simplifies the situation and ignores frictional forces, e.g. between water and tube walls, as well as the presumably small relative velocity of the water just inside the container next to the tube.)

• The net force on the water in the tube is therefore Fc - Fb = rho g y * A.

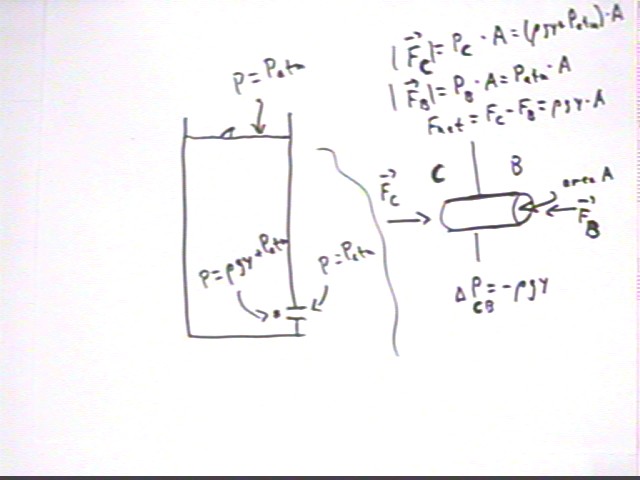
Thus we know the net force on the water in the tube.  If we know the mass of the water we can therefore find its acceleration.

• Assuming tube length L we find that the volume of the tube is A * L, so that the mass of the fluid in the tube is

mass = rho * A * L.

• We conclude that the water in the tube experiences acceleration

a = Fnet / m = rho g y * A / (rho * A * L) = g y / L.

• This expression for the acceleration is independent of the density of the fluid.  The denser the fluid the greater the fluid pressure, but also the greater the mass of the fluid in the tube.  The two effects 'cancel' and we find that acceleration depends only on gravitational acceleration, fluid depth and tube length.

We now have enough information to find the velocity of the exiting water.  We have assumed that before entering the tube the velocity of the water was zero.  Tts acceleration is g y / L and the accelerating force acts through displacement `ds = L.

• Using the fourth equation of motion vf^2 = v0^2 + 2 a `ds, with vf = v_Exit, we conclude that

v_Exit = sqrt ( v0^2 + 2 a `ds ) = sqrt ( 0 + 2 * (g y / L) * L ) = sqrt( 2 g y).

We also observed that when the system is in free fall (having been dropped or tossed upward) there is no flow from the opening.  This is because the pressure in the fluid is a result of the normal force needed to hold the fluid stationary against gravitational forces.  If the system is in free fall its acceleration is equal to that of gravity, so that the net force on the fluid is equal to its weight, and no normal force is required.  The result is zero pressure, so there is no force to accelerate the fluid out of the hole, and the flow ceases.