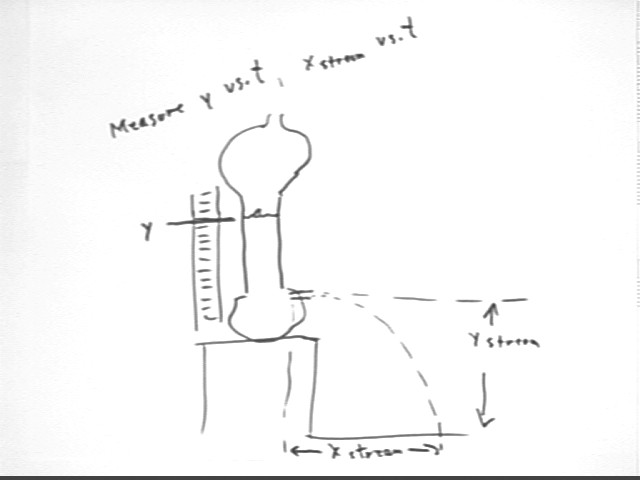
Using a container with a uniform cylindrical section and an outflow tube just below that section, fill with water to the top of the uniform section and take data sufficient to obtain a table of depth y vs. clock time t, where y is the vertical distance of the water surface above the hole.
Also take data suficient to determine xStream vs. t, where xStream is the horizontal range of the stream. Be sure to note yStream.

Analysis for Next Time:
Relevant ideas are outlined below.
As water flows out of the container the PE of the water in the container decreases.
We will express our results in terms of density rho, vertical displacement y1, acceleration of gravity g and cross-sectional area A. The short interval will occur between two clock times, which we denote as t = t1 and t = t1 + `dt, for some small `dt.
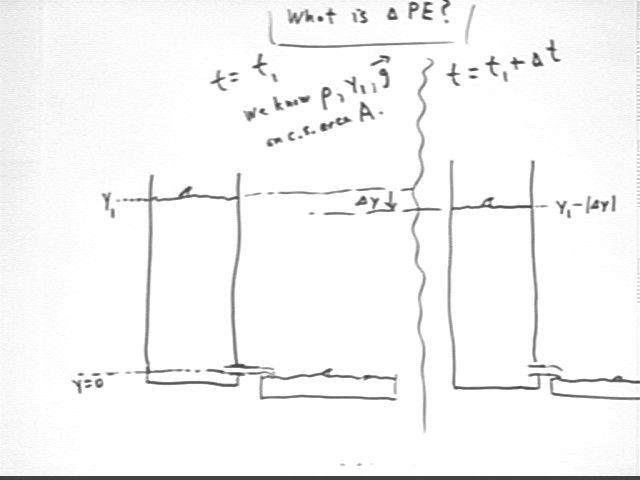
Recall that the change in the PE of a system is equal and opposite to the work done by conservative force ON the system, and is therefore equal to the work done BY the system AGAINST the total conservative force.
In this case the conservative force is that of gravity.
We will consider what happens to the PE of the system when a slice of water is vertically displaced thru `ds = -y1. We note that this displacement is in the direction of the gravitational force.
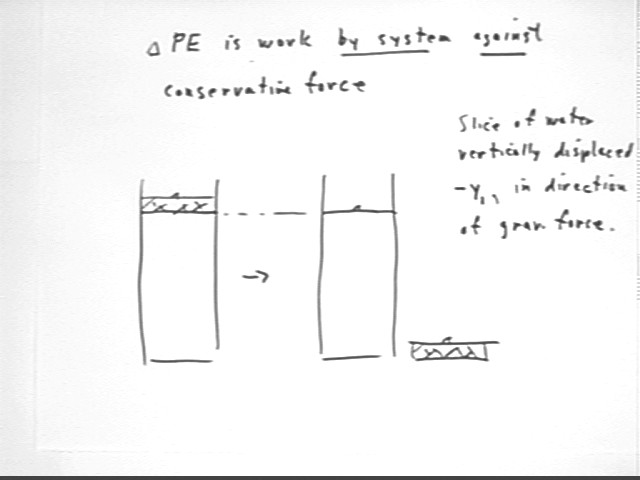
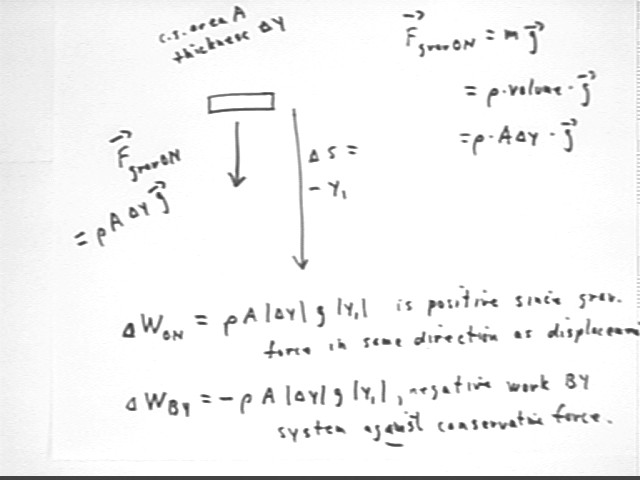
It is easier to think of the work done by gravity ON the system. The work done BY the system against gravity will be the negative of this quantity.
To find the work done by gravity on the slice we find the force exerted by gravity on the slice, and multiply by the vertical displacement, assuming a downward vertical displacement.
Our final conclusion is that FgravON, the force exerted by gravity on the slice, is
This force acts parallel to the displacement, so the work done by gravity on the system is positive and we have
It follows that the change in potential energy, which is equal to the work done by the system against gravity, is
This PE change is negative, which is consistent with our intuitive conclusion that the PE of the system decreases.
The law of conservation of energy tells us that `dKE + `dPE + `dWnoncons = 0, where `dWnoncons is the work done by the system against nonconservative forces (in this case the nonconservative forces are mostly frictional in nature, exerted between the edge of the hole and the water flowing from it).

In the system we are considering the velocity of the water in the container is presumably small so that the KE of the water in the system is negligible. In this case, if we begin with a stationary system and open the tube we will after a short time have a system with reduced PE, therefore with increased KE.
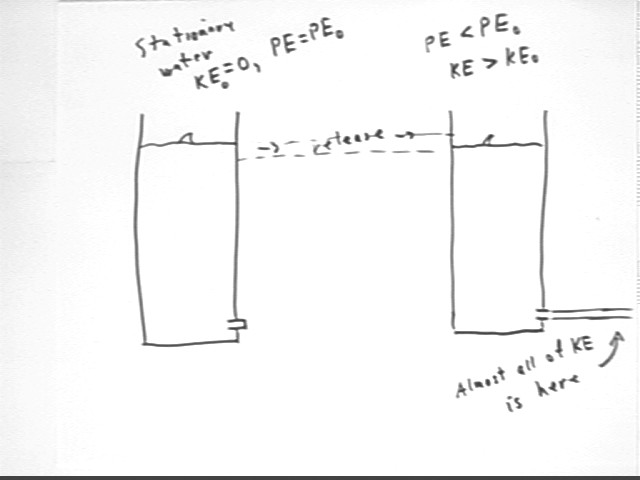
The exit velocity of the water is related to the velocity with which the water surface moves. We can determine this relationship by comparing the amount of water lost from the container to the amount of water leaving the tube in some short time interval `dt. These amount will of course be equal; what has been lost from the container has flowed through the hole. We will let v_Surface be the downward velocity of the surface of the water in the container, A_container the cross-sectional area of the container, A_tube the area of the tube through which the water exits, v_exit the velocity of the exiting water.
`dV = Acontainer * `dy = Acontainer * vSurface * `dt.
`dV = Atube * vExit * `dt.
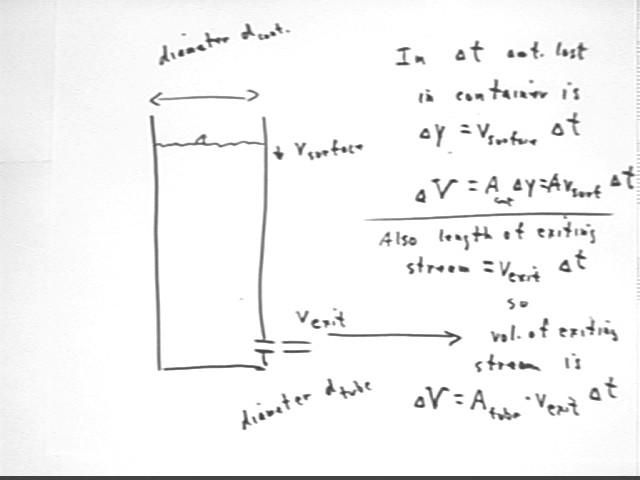
Since what comes out of the tube is equal to what left the container, the two expressions for the volume must be equal.
Setting the two expressions equal we easily solve to find that
vExit = vSurface * Acontainer / Atube.
That is, the exit velocity is equal to the velocity of the surface multiplied by the ratio of the cs areas.

Expressing this result using subscripts 1 and 2 instead of 'surface' and 'tube' we obtain the equivalent general equations
These equations apply to any incompressible fluid in a closed system. The third of these is the usual expression of this result, and is the usual form of what we call the Continuity Equation. All three forms are, of course, equivalent.