indexed
Physics II Quiz 01/22/03
Give the following results from your analysis of the experiment done with the coke bottle:
Your analysis should result in a depth vs. clock time graph that decreases at a decreasing rate (i.e., decreasing and concave upward).
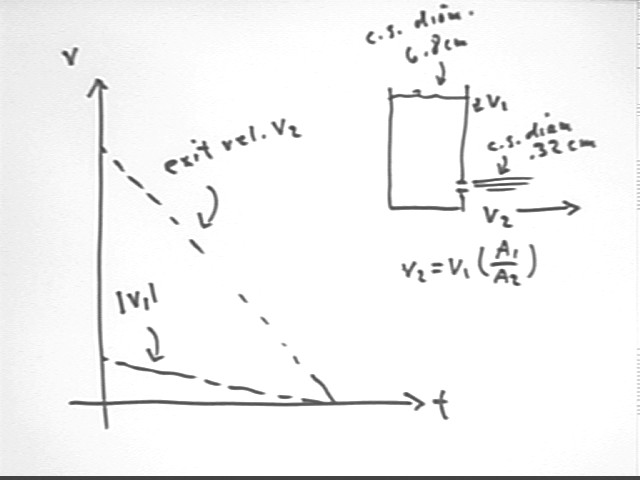
The speed v1 of the water surface is related to the speed of the exiting water by the ratio of the cross-sectional areas of the container and the tube through which water exits.
Our data will give us direct information about v1 and v2:
Since v2 = v1 * ( A1 / A2) we expect that the slope of the v2 vs. t graph will be A1 / A2 times that of the | v1 | vs. t graph.
For the given container the cross-sectional diameters of container and tube are 6.8 cm and .32 cm, so that the ratio A1 / A2 of areas will be (6.8 / .32)^2 = 450, approx..
v2 vs. t and v1 vs. t results from one group indicate a v2 / v1 ratio around 500, with a margin of error of +-150. This is consistent with the measured area ratio of 450.

Bernoulli's Equation
We apply Bernoulli's Equation to a number of situations, most related to the system analyzed in the experiment.
We note that for an (almost) incompressible fluid like water, the density rho won't be variable. For a compressible gas, rho would be variable.
We also note that the acceleration g of gravity does not vary appreciably over the scale of any water-filled system we are likely to observe.
Thus only v, h and P are considered variable for this model.
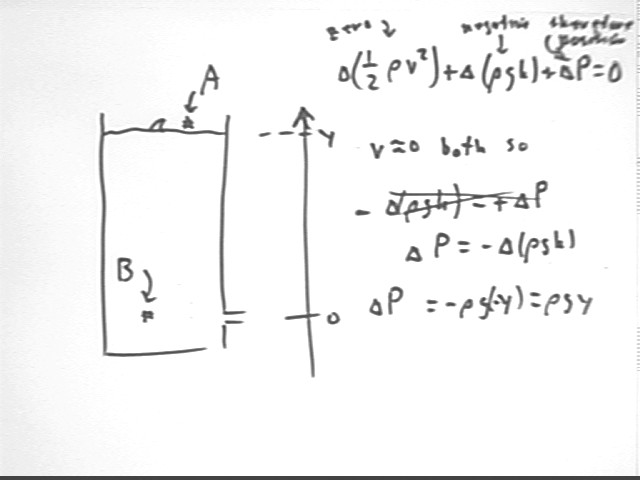
Comparing the state of the system at point A at the water surface with the state point B, where the water has just exited the container, we observe that
Thus the change in 1/2 rho v^2 is 1/2 rho vB^2, the change in rho g h is rho g * (-y) and the sum of these changes is zero.
Note that we previously obtained the same result for vB using PE to KE conversion. In fact conservation of energy is one of the principles used to derive Bernoulli's Equation.

Consider a fluid in a closed system such as the one pictured below, where a pipe is filled with water then closed. An impeller at the bottom circulates fluid around the pipe, which narrows at the indicated point. Bernoulli's Equation will tell us that the pressure in the narrow section of pipe will be less than that in the wide section. The continuity principle tells us that water is moving faster in the narrow part of the pipe.
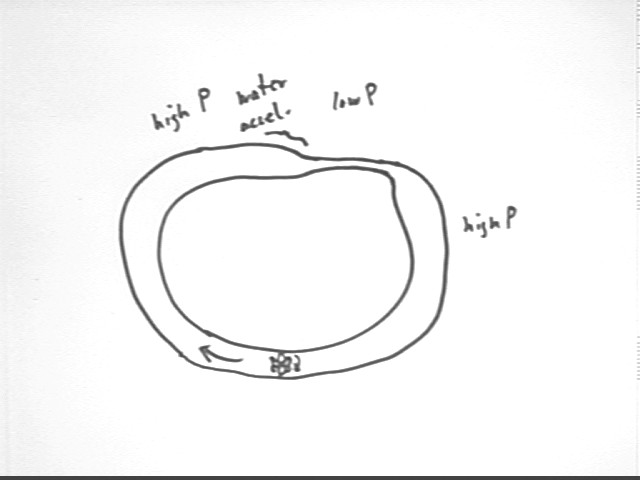
Where the pipe narrows there is negligible change in altitude h so that `d(rho g h) = 0.
v2 = A1 / A2 * v1 so that the velocity v2 in the narrow part of the pipe is greater than the velocity v1 in the wider part, so moving from point 1 to point 2 results in an increase in 1/2 rho v^2.
Bernoulli's Equation therefore tells us that since 1/2 rho v^2 increases and rho g h remains the same, the change `dP in pressure is negative.
Your textbook goes into all the details but the key is that to speed up the water we need greater pressure behind than in front, so that pressure in the wider part must be greater than that in the narrow part.
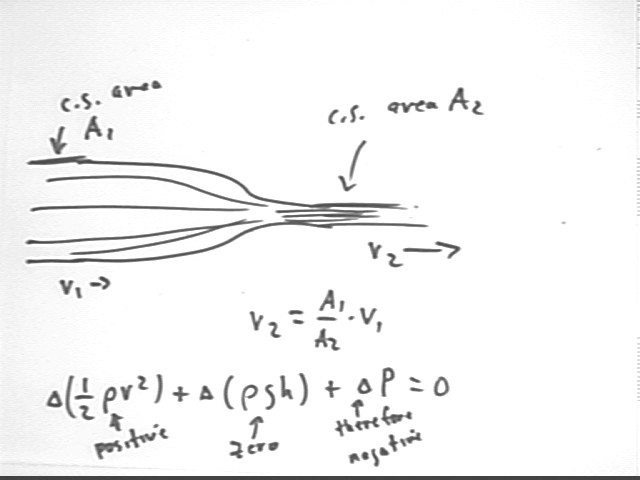
Comparing point A inside the container, at the level of the outflow, with point B directly outside we observe that
It follows that 1/2 rho v^2 must increase, so that v increases.
Noting that vA is negligible we proceed to find the expression for vB.
Recommendation: review the previous analysis, based on the work done on the 'plug' of water in the tube, of the exit velocity of the water.
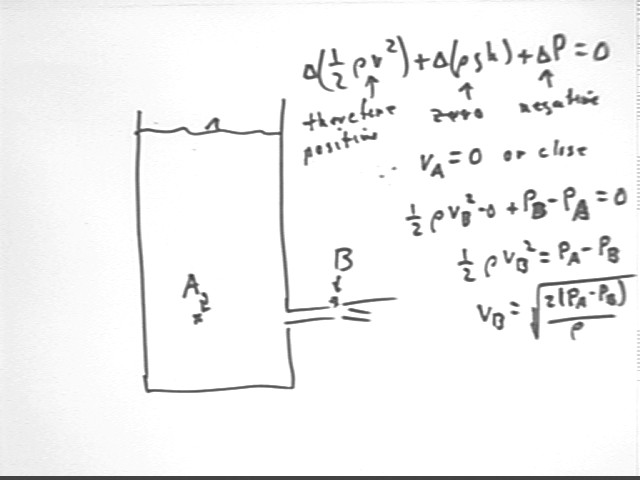
We can also compare point A at the water surface to point B at the level of the hole, but inside the container.
it follows from Bernoulli's Equation that the change `dP in pressure is positive.
Since the change in h is -y we find that the pressure change is
The pressure at depth y is greater than the pressure at the surface by rho g y, consistent with the rho g h we obtained previously by considering the weight of a water column of given height and cross-sectional area.
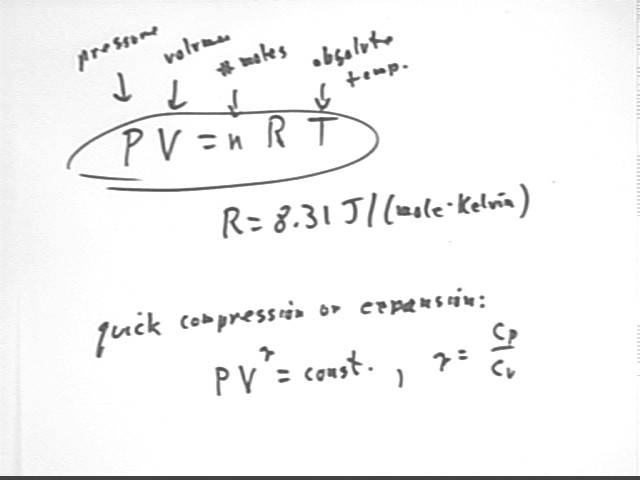
Ideal Gas Law
Squeezing a capped, empty soft drink bottle we easily experience the fact the decreasing volume is associated with increasing pressure.
According to the Ideal Gas Law, this corresponds to a decrease in V with n constant (because of the cap). If T is also constant we can conclude that P * V is constant and that P and V will be inversely proportional.
If we squeeze the bottle slowly, in a room where the temperature is the same as that of our hand, any tendency of the temperature to change will be negated by thermal energy transfers between the bottle and the room (i.e., the air in the bottle will always have time to absorb or give up enough heat to remain at constant temperature). In such a case we will have constant n and constant T and P will be inversely proportional to V.
If we squeeze the bottle quickly we are doing net work on the gas, which will increase the total KE of the gas particles, thereby increasing the temperature. In this case P, V and T will all be variable and the situation much more complicated than for constant T. The tendency of T to increase results in a more rapid pressure buildup than for constant T, resulting in the adiabatic gas law quoted, but not explained, below.
When you have completed the entire assignment run the Query program.