indexed
Physics II Quiz 01/24/03
Quiz
Quickly repeat the experiment on the energy required to melt snow and have your analysis ready for Monday.
My results: 101 ml of water at 25 C was lowered to 8.5 C by 19 ml (melted volume) of powdery snow within 60 seconds of the initial introduction of snow.
The thermal energy change of the water was
4.19 J / (kg C) * (8.5 C - 25 C) * .101 kg;
the thermal energy change of the snow was
(energy gained by melting snow) + 4.19 J / (kg C)(8.5 C - 0 C) * .019 kg.
Energy conservation tells us that
4.19 J / (kg C) * (8.5 C - 25 C) * .101 kg + (energy gained by melting snow) + 4.19 J / (kg C) (8.5 C - 0 C) * .019 kg = 0.
Solving for energy gained by melting snow we have
energy gained by melting show = -4.19 J / (kg C) * (8.5 C - 25 C) * .101 kg - 4.19 J / (kg C)(8.5 C - 0 C) * .019 kg = 6.3 J.
6.3 J of energy are thus required to melt .019 kg of snow. The energy per kg required to melt the snow is thus
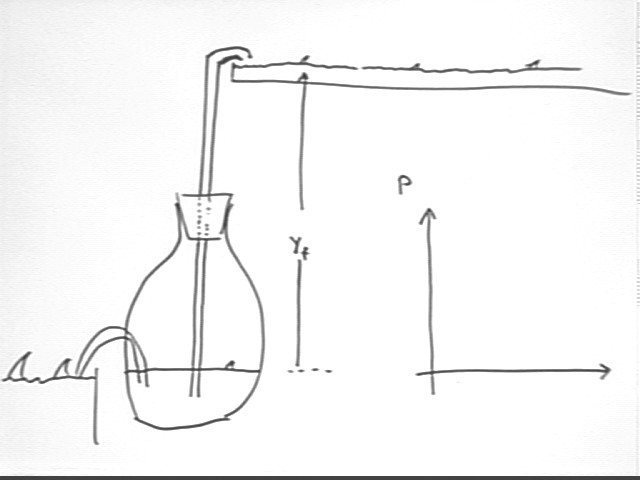
If the stream of water exiting a container in an initially horizontal stream has a horizontal range of 30 cm from an altitude of 90 cm, and if at this instant the water surface is descending at 1.5 millimeters per second, then what is the ratio of the cross-sectional area of the container to the area of the exit hole?
We find the velocity of the horizontal stream by a projectile analysis. The ratio of areas is the inverse ratio of velocities.
A range of 30 cm for a fall of 90 cm implies time of fall `dt = sqrt( 2 * .9 m / (9.8 m/s^2) ) = .43 sec, approx..
A horizontal displacement of 30 cm at constant velocity in .43 sec implies velocity 30 cm / (.43 sec) = 70 cm/s, approx..
The ratio of exit velocities is therefore 70 cm/s / (.15 cm/s) = 470.
Thus the cross-sectional area of the container is about 470 times that of the hole.
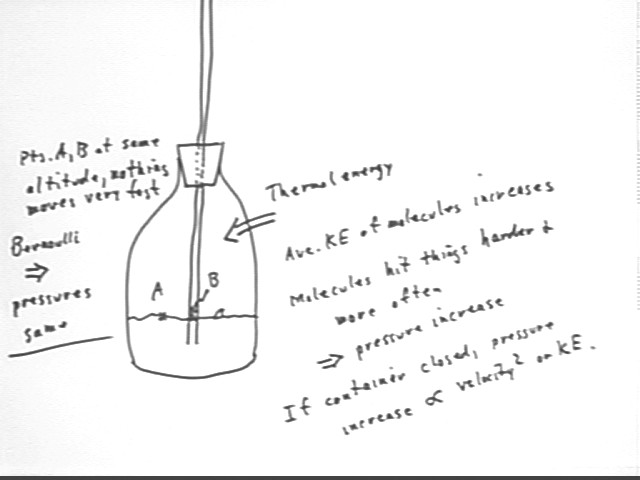
In the pictured container, points A and B are at the same altitude and we assume a slow process so that the velocities are insignificant. Thus `d(rho g h) and `d(1/2 rho v^2) are insignificant, and the pressure at A must equal the pressure at B.
If we increase the pressure at A, the only way pressure at B can equalize is for water to rise in the tube.

Suppose that we wish to lift water from one large reservoir to another which lies at altitude yf relative to the first. If the tube ends at altitude yf relative to the lower water level the the following observations hold:
The process of lifting the water increases the PE of the system. This required the addition of thermal energy to the system.
As the principle of energy conservation leads us to believe, we expect that the work done to lift the water will be less than the thermal energy put into the system.