Physics II Class 01/27

Physics II Quiz 01/27/03

Quiz

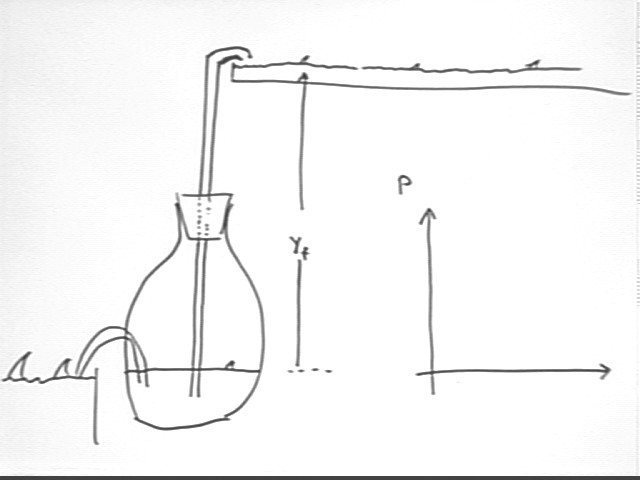
Consider the system indicated below.

• If we have an unlimited supply of thermal energy, is it possible to continue adding thermal energy to the gas in the closed system until we have lifted as much water as we desire, no matter how much we might wish to lift?  If not explain why not.

The expansion of the gas is limited by the max temperature of the thermal energy source.

Once we get to max expansion we gotta cool off again if we want to pump more water.

• Suppose the graph at lower right represents pressure P vs. volume V of the air in the system.  Assume that the vertical tube is very thin.  Starting with the system at atmospheric pressure, and continuing until a substantial amount of water has been lifted, what would a graph of P vs. V look like?
• Explain what happens to the thermal energy added to the system, both during the phase where water rises in the tube and during the phase when water exits the top of the tube..

We see that when thermal energy is put into this system in the specified manner the result is that mechanical work is done by the system and thermal energy is taken from the system in the cooling process.

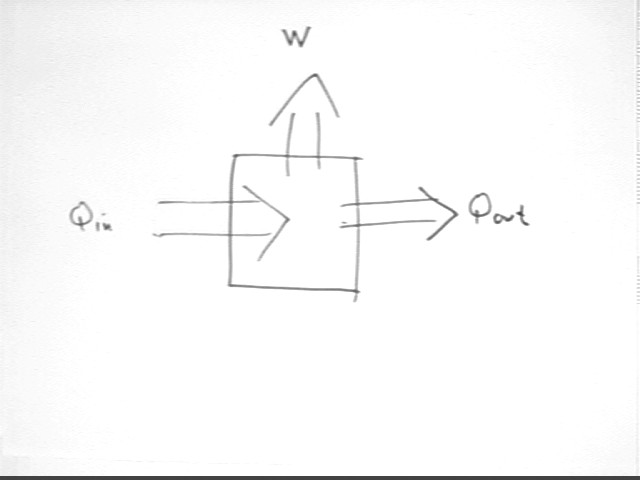
To better understand the system, and so that it will be possible to analyze the energy exchanges that take place, we must understand more precisely what happens to the energy that goes into the system and how the system is affected.

We begin by considering a closed container containing N 'billiard-ball' particles each of mass m, with all particles stationary.  This corresponds to an initial state with no thermal energy; we say that the system is initially at absolute zero with respect to thermal energy.

We think of adding a quantity Q of thermal energy.  

• This makes the total thermal energy of the system U = Q.  Note that we use U to stand for the total internal energy of the system.
• The thermal energy will on the average be distributed equally between the particles so that, on the average, each particle has thermal energy Q / N (or, using U for total internal energy, U / N).

It follows that on the average the velocity of a particle is v = sqrt( 2 U / (m * N ) ).

We will see that knowing the average velocity of a particle and the volume of the container we can find the average pressure exerted by the molecules.

From the Introductory Problem Sets you are familiar with the fact that a single particle of mass m bounding back and forth between walls C and B of a container with velocity vx will exert force Fave = 2 * KEx / L on wall C.

If there are many molecules in the container they will collide with one another and on the average the x, y and z velocities will be equal, with vAve^2 = vxAve^2 + vyAve^2 + vzAve^2.  

• It follows that vxAve^2 = vyAve^2 = vzAve^2 = 1/3  vAve^2.
• From this it follows that KExAve = 1/3 KEave, where KEave is the average KE of a particle in the system.

We therefore conclude that the force Fave exerted by a single particle is 2/3 KEave / L.

• If the cross-sectional area of the container, in the direction perpendicular to the x direction, is A then the average pressure exerted by that particle is Pave = Fave / A = 2 KEave / V.
• The total pressure exerted by N molecules is therefore Ptotal = N * 2/3 KEave / V = 2/3 * N * KEave / V.

Since KEave = U / N we can rewrite this as

• Ptotal = 2/3 * U / V.

Rearranging these relationships we have

• P V = 2/3 * N * KEave  and
• P V = 2/3 * U.

Since PV = n R T = N k T, with n, N, R and k as indicated below, it follows that 

• T = 2/3 * KEave / k and that
• KEave = 3/2 k T,

where KEave is the average KE of a particle.

For example, if 1 amu = 1.7 * 10^-27 kg, what is the ave velocity of this particle at T = 300 K?

We have KEave = 3/2 k T so

.5 mvAve^2 = 3/2 k T and

vAve = sqrt(3 k T / m) = sqrt((3 * 1.38 * 10^-23 J / (particle K) * 300 K ) / (1.7 * 10^-27 kg) ) = sqrt(7.2 * 10^6 m^2/s^2) = 2700 m/s.  

The mass of an atom is the number of amu's equal to its atomic mass number.  The atomic mass number of oxygen is 16.  What would be the average velocity of a single oxygen molecule at 300 K?

• Noting that v = sqrt( 3 k T / m) and that m = 1 amu implies velocity around 2700 m/s, we conclude that m = 16 amu would result in sqrt(1/16) = 1/4 the average velocity of a 1 amu particle, or 1/4 * 2700 m/s = 675 m/s.

Oxygen isn't normally monatomic.  What is the average KE of a diatomic oxygen molecule?

• A diatomic oxygen molecule has m = 32 amu, so its ave velocity will be sqrt(1/32) = 1 / (4 sqrt(2) ) = .17, approx., the ave velocity of a 1 amu particle.  This gives us an estimate of about 2700 m/s * .17 = 470 m/s.