THESE FIGURES ARE CURRENTLY UNEDITED. EDITING WILL BE COMPLETE ASAP.
Physics II Quiz 01/29/03
Quiz
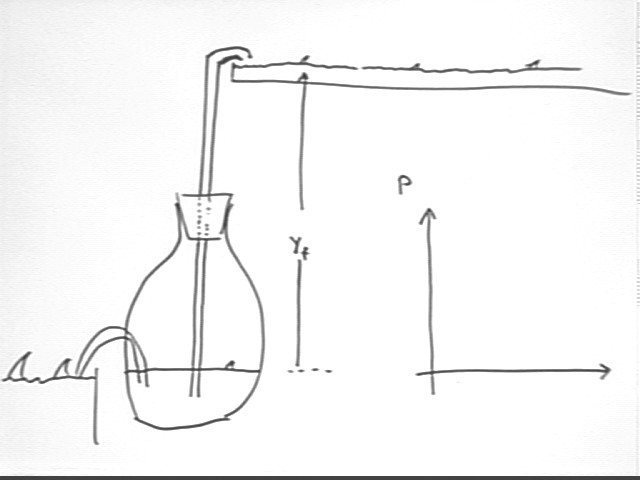
Consider the system indicated below.

When thermal energy is first introduced the result is a pressure buildup without significant change in volume. Note that there is no significant volume change until the thin tube is filled.
When the tube becomes full water begins flowing out of the system, allowing the gas to expand. Since the height of the water column no longer changes the pressure in the system will remain unchanged.
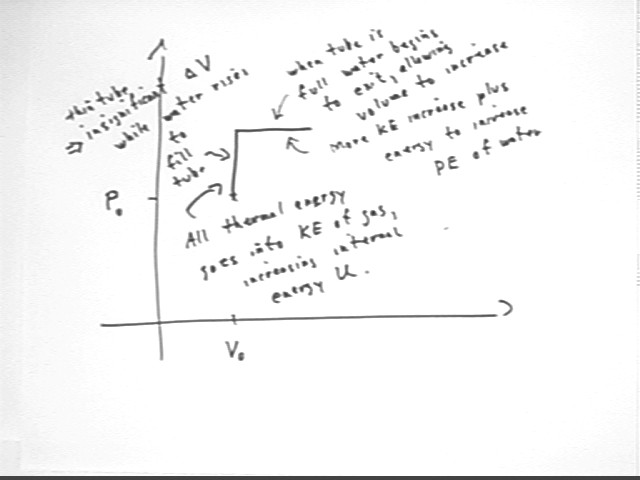
As long as volume is constant the thermal energy going into the system all goes into increasing the KE of the molecules.
When the gas begins to expand it does work against the water surface in the container, some but perhaps not all of which goes into lifting the water that flows from the top of the tube. The increasing pressure is the result of more rapidly moving molecules so energy also goes into increasing the KE of the molecules.
These ideas are indicated in the figure above.
Once the system has reached the maximum temperature possible with the source of thermal energy, it will cease to expand and no more water can be pumped until we return the system to its initial state. We now analyze how we might complete the cycle in order to pump more water.
To return the system to its original state the pressure and temperature must both be decreased. There are several ways to do this:
We might open a valve and allow the system to expand suddenly, which will have the effect of returning the system quickly to its original pressure and also lowering the temperature, though not to the original temperature. This would be an adiabatic expansion. To analyze an adiabatic expansion requires more information than we have at present.
Another alternative would be to cool the system. However this would require that we decrease the volume of the system, which would be feasible by allowing more water to enter, but the analysis would also be more complicated than the alternative we will use here.
Among other feasible alternatives we will choose to allow the system to first expand at constant temperature until it is again at its original pressure, and then contract it at this pressure while cooling it. This is not generally the most practical alternative but it is probably the easiest to analyze.
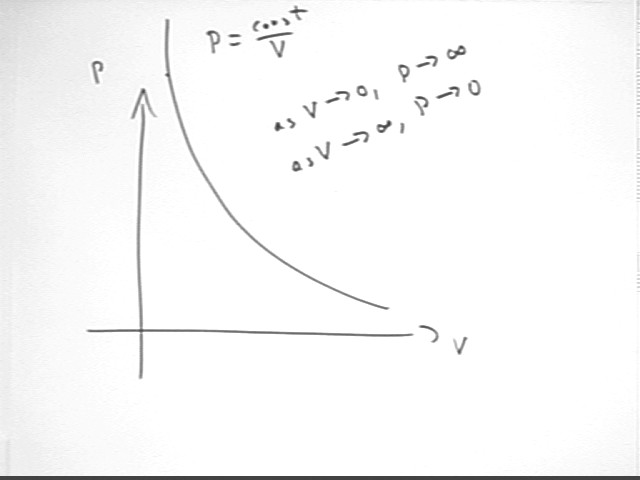
We first note that if we keep the temperature of a closed system constant while allowing pressure and volume to change, we have constant T and constant n, so that n r T remains constant and we therefore have P = nR T / V = constant / V:
P = constant / V
We graph the general shape of the P vs. V curve for constant T and n:
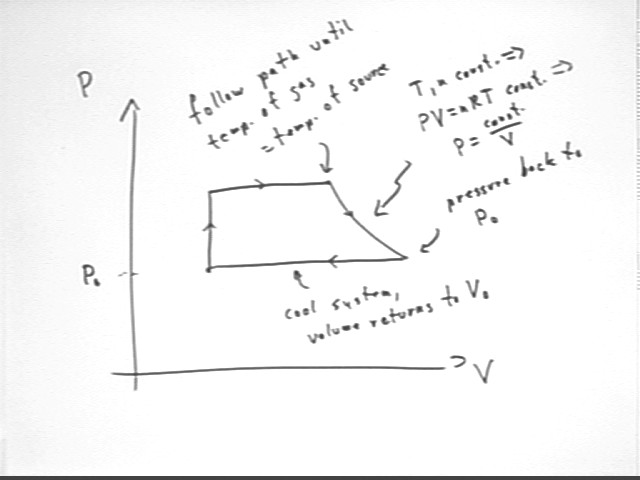
Our P vs. V diagram for the process will therefore look something like that depicted below:
Having reached maximum temperature after the constant-volume heating and constant-pressure expansion we allow the system to expand slowly while remaining in contact with the thermal source so that its temperature remains constant.
The cycle therefore follows the curve P = const. / V as indicated, continuing along this path until pressure has returned to the original pressure P0.
We then cool the system at this pressure, allowing the temperature and therefore the volume to return to their original values.
We now assume a thermal energy source at 350 K and analyze a system with initial volume 3 liters and initial temperature 300 K, in which we allow pressure to increase at constant volume until we can support the 70 cm column of water, then allow the system to expand until we reach a maximum temperature of 350 K.
The first part of the cycle is shown below, where pressure is allowed to increase until it will support the water column.
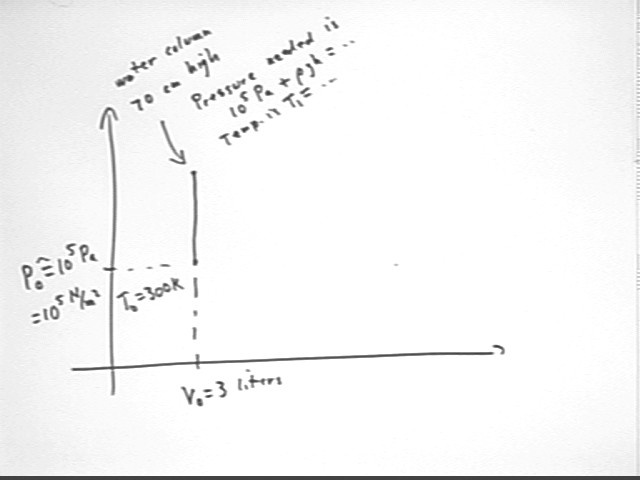
To find the state of the system at this point we first determine the pressure required.
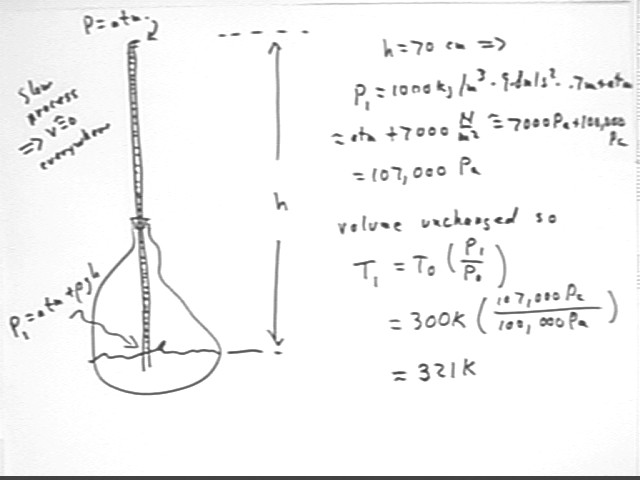
The pressure at the top of the full tube will be atmospheric pressure.
The pressure at the bottom of the tube will be greater than atmospheric pressure by `dP = rho g h.
A simple calculation tells us that the pressure in the container must therefore be P1 = Patm + rho g h = 107,000 Pa, approx.. This assume atmospheric pressure 100 kPa.
Since volume is unchanged the new temperature will therefore be T1 = T0 * (P1 / P0) = 300 K * (107 kPa / (100 kPa) ) = 321 K.
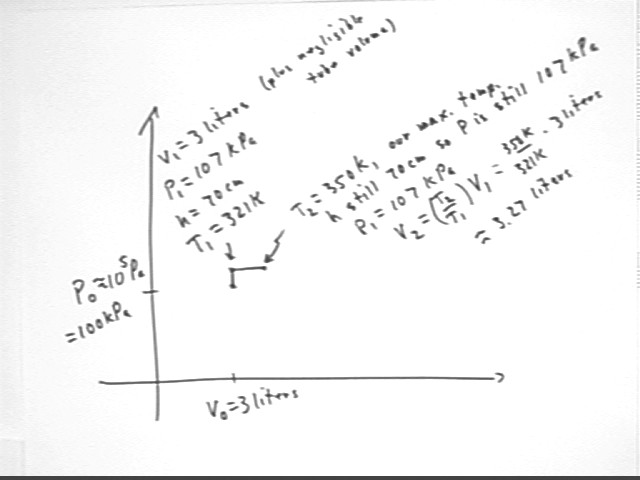
The system is then allowed to expand at constant pressure until temperature is T2 = 350 K, the max possible temperature for the thermal source.
The resulting volume will be V2 = V1 * T2 / T1 = 3 liters * (350 K / (321 K) ) = 3.27 liters.
This information is depicted below.
We now ask how much energy is required to accomplish this much of the cycle:
Recall that for an ideal monatomic gas the KE per particle is 3/2 k T.
It follows that the total KE of the system is N * 3/2 k T = 3/2 N k T, where N is the number of particles in the system.
Since N k = n R, where R is the gas constant and n the number of moles, the total KE of the system is also equal to 3/2 n R T.
Using U to denote the total internal KE of the system we therefore have
U = 3/2 n R T.
Since PV = n R T we also therefore have
U = 3/2 P V.
For the above system in its initial state we easily calculate the internal energy, obtaining U = 450 J, approx..
The final state, as shown below, has U = 530 J approx..

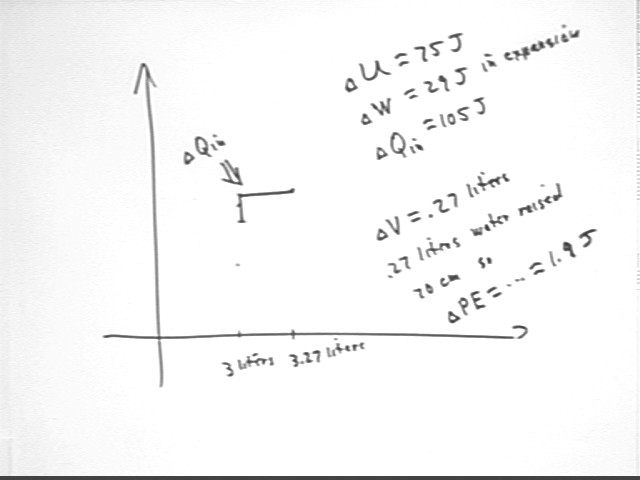
Thus the internal energy increases between initial and final state by approximately 80 Joules.
A more accurate calculation indicates that the internal energy increase is closer to 75 Joules.
The work done in an expansion is equal to the area under the corresponding P vs. V graph.
In this case the region undero the P vs. V graph extends from V = 3 liters to V = 3.27 liters, giving the region a width of .27 liters, and has a constant 'height' of 107 kPa.
The area of this region is thus about .27 liters * 107 kPa = 29 Joules.
The thermal energy supplied to the system was therefore the sum of the 75 J required to increase the internal energy of the system, and the 29 J required to do the work of expansion.
We conclude that the thermal energy `dQin supplied to the system was about 75 J + 29 J, or approximately 105 J.
During the process .27 liters of water was raised to an altitude of .70 meters, resulting in a potential energy increase of about .27 liters * 1 kg / liter * 9.8 m/s^2 * .70 m = 1.9 Joules.
If no further thermal energy is supplied to the system as it completes the rest of its cycle, we conclude that the efficiency of the cycle is
efficiency = mechanical work accomplished / thermal energy required = 1.9 J / (105 J) = 1.8%, approx.
This seems like a pretty low result but note that most engines run below 20% efficiency, and the 1.8% efficiency is not bad if the energy is cheap enough, which can sometimes be the case with thermal energy.
Note also that as we can see by analyzing a similar system at a higher maximum temperature, a hotter source of thermal energy would permit more expansion and more PE increase, and a net increase in efficiency.
When you have completed the entire assignment run the Query program.