Quiz 0131
Step 1: For each question write down, using numbers and/or symbols and/or graphs, how you're gonna solve the problem.
Step 2: Go back and solve as many problems as you can. You can take the density of water to be 1000 kg / m^3 and atmospheric pressure to be 100 kPa.
How many moles of a gas are there in a 5 liter closed container at atmospheric pressure and temperature 450 Celsius?
Use PV = n R T, solve for n.
n = P V / (R T) = 100 kPa * 5 liters / (8.31 J/(particle K) * (450 K + 273 K) = .08 moles, approx.
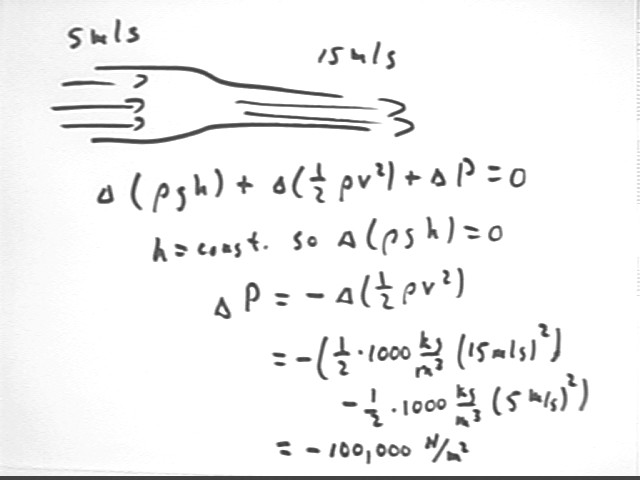
How much pressure loss will occur if water in a closed system changes velocity from 5 m/s to 15 m/s with no significant change in altitude?
Use Bernoulli's Equation `d( .5 rho v^2) + `d ( rho g h ) + `d P = 0 with h = 0 so

What pressure is required in a system originally at atmospheric pressure in order to raise water from initial altitude 0 to altitude 8 meters?
`d( .5 rho v^2) + `d ( rho g h ) + `dP = 0 with v = 0 to get
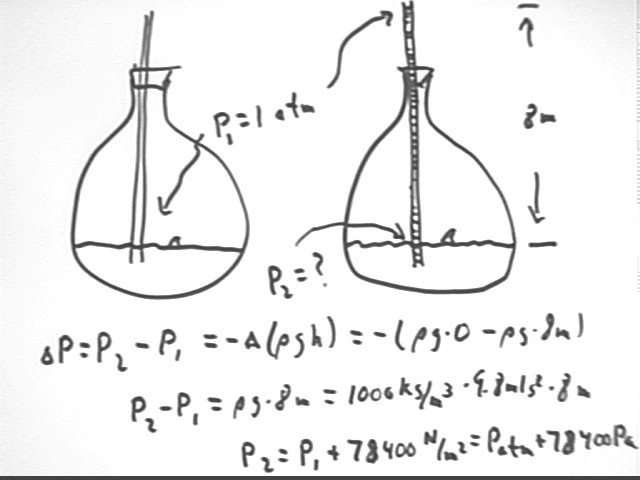
To what temperature must a gas in a closed system be raised, starting at 300 K, to lift water up a thin tube of length 3 meters, with the system originally at atmospheric pressure?
Find pressure required. Since container is closed and tube is thin only temperature and pressure change, so then use pressure vs. temperature relationship P2 / P1 = T2 / T1.
Additional pressure required is 29,400 Pa so P2 = 100 kpa + 29.4 kPa = 129.4 kPa and P1 = 100 kPa.
So T2 = T1 * (P2 / P1) = 300 K * (129.4 kPa / (100 kPa) ) = 390 K.
What is the translational KE per particle in a gas which occupies 3 liters at 300 Kelvin and atmospheric pressure? Translational KE is the KE of associated with motion through space, as opposed to vibrational motion or spinning motion.
Translational KE per particle is 3/2 k T.
At 300 K we have 3/2 k T = 6.21 * 10^-21 J.

How many particles are present in a gas which occupies 3 liters at 300 Kelvin and atmospheric pressure? What therefore is the total KE of all these particles?
Find # moles as in first step, but for 300 K. Multiply by Avagadro's Number. Then multiply by the KE per particle.
As shown in the lower half of the figure above
As shown in the first two lines of next figure
What will be the total translational KE if the system in the preceding problem is raised to 450 K?
Same analysis as in preceding but recalculate KE = 3/2 k T for new T.
As shown in the next three lines of the figure, we'll end up with T2 / T1 = 450 / 300 = 1.5 times the total KE, or about 1.5 * 450 J = 675 J approx..
How much energy does it take to raise the translational KE of the particles in the preceding system from 300 K to 450 K?
We simply subtract the KE at 300 K from the KE at 450 K:
How many Joules per mole are required to raise the translational KE of the particles in the preceding system by 1 degree Kelvin?
Divide the preceding by the number of moles, and by the 150 degree K change to get the number of Joules per mole, per Kelvin. The result is called the molar specific heat.
We get
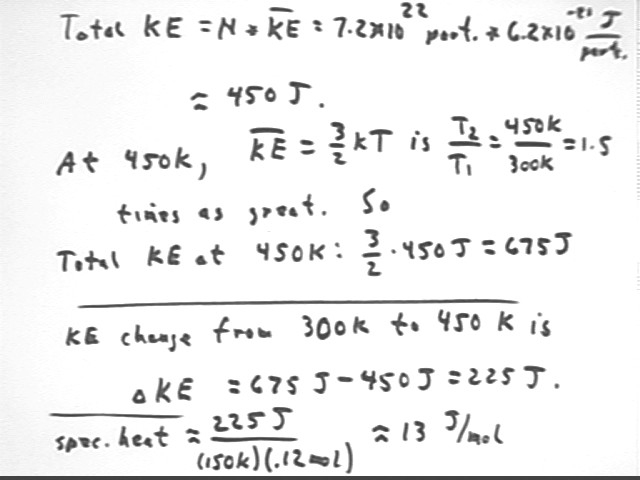
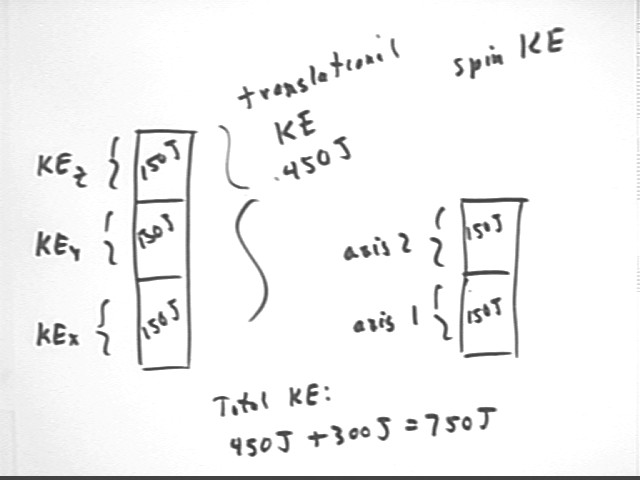
How much of the total translational KE of the system in the preceding questions is associated with motion in the x direction, when that system is at 300 K? How much with the y and z directions?
Total translational kinetic energy is .5 m vAve^2.
vAve^2 = vxAve^2 + vyAve^2 + vzAve^2.
vxAve = vyAve = vzAve so
Thus since KE = .5 m v^2 we have
If the molecules in the system are diatomic then they can spin about two independent axes. The spin about each of these axes has an average total KE equal to the KE in the x direction. At 300 K how much KE will the molecules in the system of the preceding problems have, assuming that the gas is diatomic? How much total KE change is there in the molecules as the system's temperature increases from 300 K to 450 K?
As depicted in the figure below the total translation KE can be equally divided, on the average, among the three independent directions of space, with KEx = KEy = KEz = 1/3 KEtranslational = 1/3 * 450 J = 150 J.
Each of the two directions of rotational motion has the same KE, so that the total KE is 450 J + 300 J = 750 J.