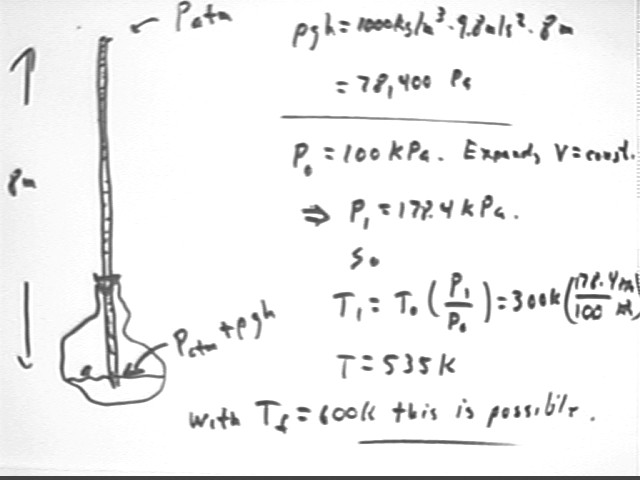
A diatomic gas which initially occupies 250 liters at 300 Kelvin and atmospheric pressure is to be used to pump water up to a height of 8 meters. It is possible to heat the gas to a maximum of 600 K, and the gas can be cooled to 300 K.
Using the same procedures as in previous classes we find that the water column reaches the 8 m altitude at T1 = 535 Kelvin.

We could find the ave translation KE per particle using KEaveTrans = 3/2 k T; we obtain KEaveTrans = 4.9 * 10^-21 Joules, approx..
We could then note that the total translational KE is N * KEaveTrans, where N is the number of particles present. So we get
However N k is the same as n R so we find that the total translational KE is
and since PV = n R T we have
From this we find the translational KE of the gas in the first and second states, and subtract to find that the change in translational KE is about 27,900 J.
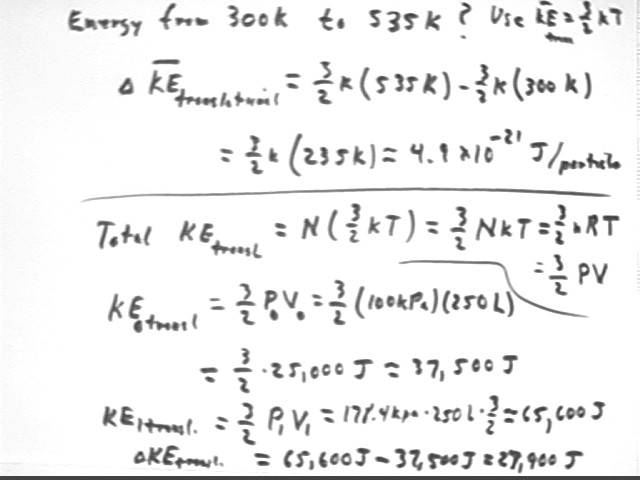
Between these two states there is negligible expansion because of the thinness of the tube. There is therefore negligible work done in the expansion.
However since the system consists of mainly diatomic molecules there is kinetic energy associated with the rotation of those molecules. We recall that 1/3 of the total translational KE is present in each of the 3 independent directions of space, and that this same KE is present in rotation about each of the two independent axes. So the total KE of the system is
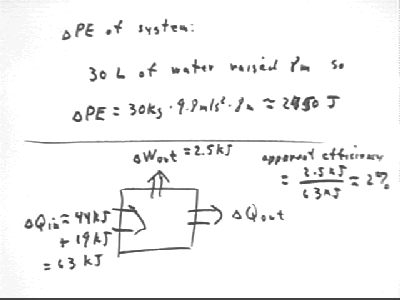
This gives us a total KE of about 44,000 J.
This is the internal energy
of a diatomic gas.

Repeating the analysis from previous classes we find that V2 = T2 / T1 * V1. For the present parameters of the system we find that V2 = 280 liters, approx.
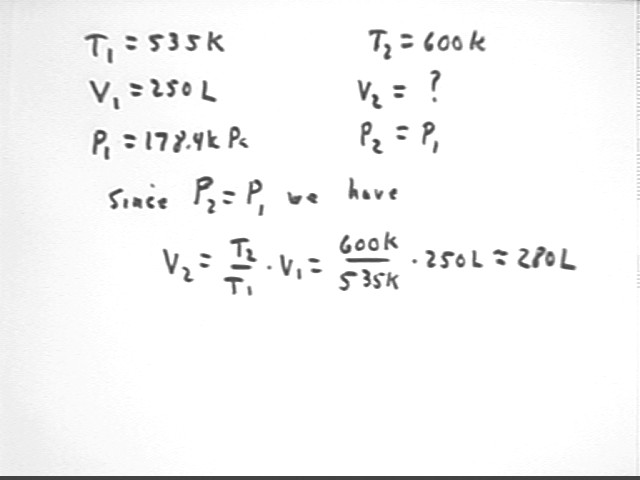
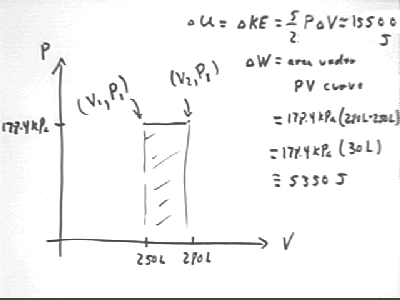
The change in the internal KE is the change in U = KE = 5/2 P V; since P is constant this change is `dU = 5/2 P * `dV so we have
The thermal energy necessary to expand the gas is the area beneath the P vs. V curve. This region is rectangular so we easily find the result to be 5330 J.
A total of 5330 J + 13500 J = 19,000 J, approx. is transferred during the expansion.
This is in addition to the approximately 44,000 J transferred as pressure built at constant volume.
To we have
30 liters of water, mass 30 kg, was lifted 8 meters, increasing the PE of the system by 2450 J, approx..
Apparent efficiency is
Note that kJ means kiloJoules, or thousands of Joules.
If the gas in this system is now allowed to expand isothermally (very slowly while maintaining its temperature) until its pressure has returned to atmospheric, what is the final volume of the gas?
Since PV is constant for an isothermal expansion of a closed system we obtain the new volume V3 = P2 / P3 * V2 = 500 liters.

In the isothermal expansion how much thermal energy had to be added to the system?
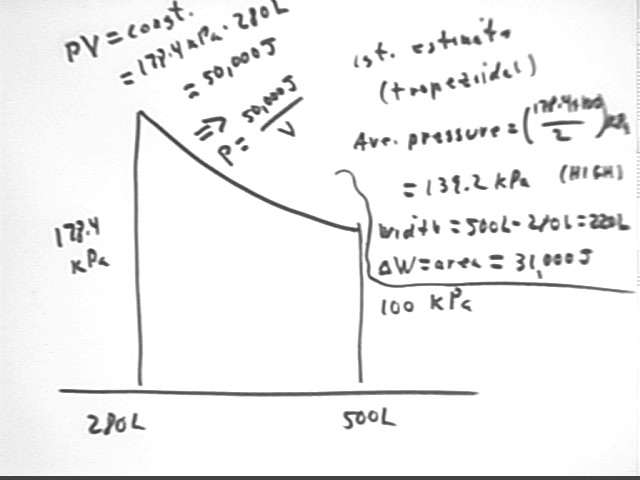
We will sketch the P vs. V curve from state 2 to state 3 and estimate the area beneath the curve.

Since PV is constant we use the pressure and volume at state 2 to evaluate this constant, obtaining P V = 50,000 J so that
We sketch a graph to represent this function.
A first estimate of the area approximates the region beneath this curve by a trapezoid and gives us total area representing about 31,000 J.
We could approximate the region by partitioning the interval from 280 liters to 500 liters into smaller intervals, evaluating P = 50,000 J / V at each point. We would end up with a larger number of trapezoids, for each of which we could find the area. Adding the areas would give us a more accurate approximation.
University Physics students note that we can easily integrate P = 50,000 J / V with respect to V, from V = 280 liters to V = 500 liters. You should verify that the result is very close to 29,000 J, which is about 6% less than the result of the trapezoidal approximation.
Does this result imply a different value than before for the efficiency of the process?
This does imply a different efficiency because we have now transferred an additional 30,000 J, approx., into the system. We would have to recalculate the efficiency based on the same PE change, but on the greater total amount of thermal energy transferred.
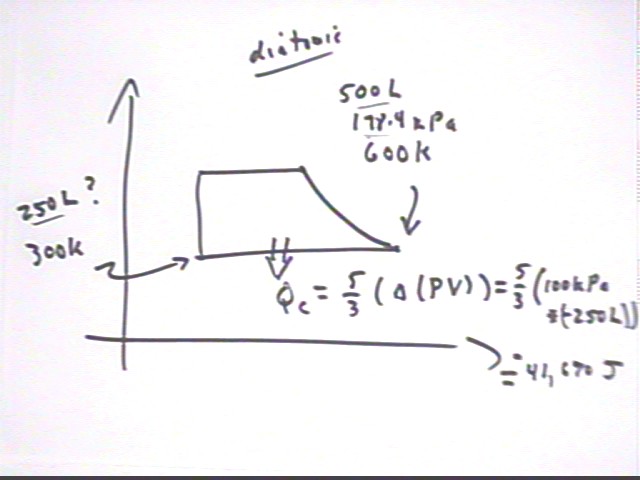
If the gas is then cooled back to its original temperature without changing the pressure of the system how much energy must be taken from the system?
In cooling the gas we have to decrease the KE of the system and also carry away the additional thermal energy that will result from compressing the gas.
The change in internal KE at constant pressure is 5/2 P `dV, which in this case is 5/2 (100 kPa) * (-250 liters) = -62,500 Joules.
The work done by the system is equal to the area under the curve, which since we are moving in the negative horizontal direction will be negative. This work is `dW = P `dV = 100 kPa * (-250 liters) = -25,000 Joules.
We must therefore take from the system a total of 62,500 J - 25,000 J = 87,500 J.
When you have completed the entire assignment run the Query program.