Problem: We refer to the number of volts / meter (or alternatively the number of Newtons/Coulomb) at a point as the electric field strength at that point. In a certain region, the electric field is uniformly equal to 34 volts / meter.
Find
the force exerted on a charge of 36 `microC in the vicinity of this field
the work done by the field in moving this charge .1800 meters in the direction of the field
the potential gradient dV/dx of the field
the force per unit charge exerted by the field."
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution
Solution: An electric field of 34 volts/meter is equivalent to 34 N / C. Thus the 36 `microC charge will experience a force of
36 `microC ( 34 N/C) = .001224 N.
The work done over a .1800 meter displacement in the direction of the field is
( .001224 N)( .1800 meters) = .0002203 Joules.
The potential gradient is just the 34 volts / meter; the potential gradient and the electric field strength are identical.
The force per unit charge is just 34 N/C. The electric field strength is the force per unit charge.
Generalized Response: A charge q in an electric field E will experience a force of q E, as is obvious from the units (E is measured in volts/meter, the same as Newtons/Coulomb, while q is measured in Coulombs). The work done in moving the charge through a displacement ds in the direction of the field will have magnitude |W| = |q E | ds. The potential difference has magnitude |W| / q = | E | ds. The potential gradient is potential difference/displacement, so has magnitude | E | ds / ds = | E |. Since E measures Newtons/Coulomb, it measures force/unit charge.
.
.
.
.
.
.
.
.
.
.
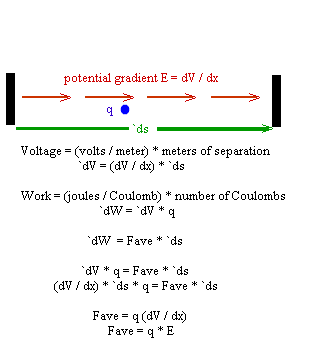
Figure description: The figure below shows a charge q moving through a displacement `ds in the direction of a potential gradient dV / dx. The potential difference will be the product of the potential gradient and the displacement: `dV = dV / dx * `ds. The work done on the charge is therefore `dW = q `dV; this work is also the product `dW = Fave * `ds of the average force on the charge and the displacement. Setting these two expressions for work `dW equal we arrive at the conclusion that Fave = q dV/dx = q E.
E = dV / dx is called the electric field. Since E = Fave / q, we see that the electric field E is the force per unit charge experienced by a charge.