Problem: To move .5250 Coulombs of charge from point A to point B in 1.8 seconds requires an average power of .9000 watts. What is the magnitude of the potential difference between A and B?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: Potential difference is measured in Volts, or Joules per Coulomb. Let's look at the Joules and the Coulombs per second: The work is being done at the rate of .9000 J/s, while charge is passing at ( .5250 C)/( 1.8 sec) = .2916 C/s. Thus .9000 J must correspond to .2916 C, so that the potential difference must be .9000 J / ( .2916 C) = 3.086 J/C, or 3.086 Volts.
Generalized Response:
.
.
.
.
.
.
.
.
.
.
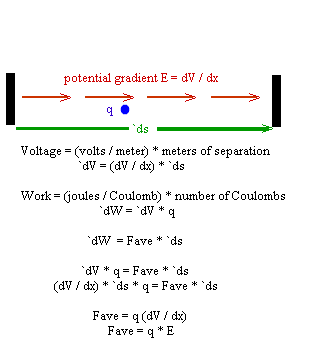
Figure description: The figure below shows a charge q moving through a displacement `ds in the direction of a potential gradient dV / dx. The potential difference will be the product of the potential gradient and the displacement: `dV = dV / dx * `ds. The work done on the charge is therefore `dW = q `dV; this work is also the product `dW = Fave * `ds of the average force on the charge and the displacement. Setting these two expressions for work `dW equal we arrive at the conclusion that Fave = q dV/dx = q E.
E = dV / dx is called the electric field. Since E = Fave / q, we see that the electric field E is the force per unit charge experienced by a charge.