Problem: By analogy with the gravitational field, we think of a point charge q as the source of flux, analogous to a point light source. This flux spreads out over concentric spheres, with uniform density (analogous to brightness) on any such sphere. The flux through every concentric sphere is the same, and is equal to 4`pi kq. The constant k is called the electrostatic force constant, and is equal to approximately 9.0 x 10^9 N m^2 / C^2. The magnitude of the electric field at a point is simply the flux per unit area at that point. The flux spreads outward from a positive charge and inward toward a negative charge. The electric field is a vector which points in the direction of the flux.
Find the flux of a 26 `microC charge, and the magnitude of the electric field due to the charge, at a distance of 2.2 meters from the charge.
Find an expression for the magnitude of the electric field produced by a charge q at a distance r from the charge. Use this expression to determine the following:
The ratio of electric fields that results from doubling the distance r.
The ratio of electric fields that results from doubling the charge q with no change in r.
The ratio of electric fields that results from doubling both the distance and the charge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution
Solution: A charge of 26 `microC produces a flux of 4`pi kq = 4`pi (9 x 10^9 N m^2 / C^2)( 26 `microC) = 2940 x 10^3 N m^2 / C. At a distance of 2.2 meters from the source, the flux is spread over a sphere of radius 2.2 m with total area 4`pi r^2 = 4`pi ( 2.2 m)^2 = 60.82 m^2. The flux per unit area is therefore
flux / area = ( 2940 x 10^3 N m^2 / C) / ( 60.82 m^2) = 48.33 * 10^3 N / C.
This is the magnitude of the electric field produced by the charge at the 2.2 meter distance.
Note that we can find the force on a charge q in the vicinity of this field by multiplying q by 48.33 N/C. If q is expressed in Coulombs, then this product will be in Newtons.
If we double the distance r from a charge, the area 4`pi r^2 of the sphere over which the flux is spread quadruples. The flux will therefore be divided by four times the area, and will be only
as great as before.
If the charge is doubled, the flux will be doubled. If the distance is not changed, the field strength will be equal to a doubled flux divided by the same area. Thus the field strength will be doubled.
Doubling the distance quadruples the area while doubling the charge doubles the flux. When we divide a doubled flux by a quadrupled area we get half the former electric field.
Generalized Response: The flux of a charge Q is 4 `pi k Q. When spread out over a sphere of radius r, the flux density is 4 `pi k Q / (area of the sphere) = 4 `pi k Q / (4`pi r^2) = k Q / r^2. This is the electric field strength.At distance 2r, the field is similarly found to be k Q / (2r)^2 = (1/4) k Q / r^2, or
as great as at distance r.If charge is doubled the field will be k (2Q) / r^2, twice as great as for the original charge at this distance.If distance and charge are both doubled the field becomes k (2Q) / (2r)^2 = (1/4) k Q / r^2, have as great as for the original charge and distance.
.
.
.
.
.
.
.
.
.
.
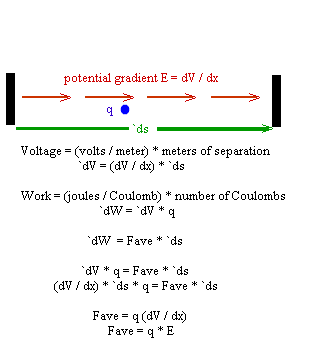
Figure description: The figure below shows a charge q moving through a displacement `ds in the direction of a potential gradient dV / dx. The potential difference will be the product of the potential gradient and the displacement: `dV = dV / dx * `ds. The work done on the charge is therefore `dW = q `dV; this work is also the product `dW = Fave * `ds of the average force on the charge and the displacement. Setting these two expressions for work `dW equal we arrive at the conclusion that Fave = q dV/dx = q E.
E = dV / dx is called the electric field. Since E = Fave / q, we see that the electric field E is the force per unit charge experienced by a charge.