Problem: The flux from a long straight uniform charged conducting wire is 4`pi kq, where q is the charge of the wire. Because of the strong repulsion of the charges, they get as far from one another as possible. The way they do this is to become equally distributed over the wire. Because of symmetry, the flux must come out of the wire at a right angle to the wire, and it must be such that a cylinder whose axis coincides with the wire experiences very nearly equal 'illumination' by the flux at every point, provided that the radius of the cylinder is very much less than the length of the wire. Near the ends of the wire, the flux comes out at different angles, with some escaping through the ends of the cylinder, and as a result the cylinder is not as 'brightly illuminated' by the flux near its ends. If the wire is very long compared to the cylinder radius, this 'end effect' is not very significant, and we can assume that practically all the flux is evenly distributed over the curved surface of the cylinder.
Suppose that a charge of 5.9 `microC resides on a wire 29 meters long.
What is the total flux generated by the charge.
What is the total surface area of a cylinder of length 29 meters, open at the ends, which symmetrically surrounds the wire at a uniform distance of .2100 meters?
What is the magnitude of the electric field at a point .2100 meters from the wire, and not close to either end?
Use these ideas to find the electric field at a point .05000 meters from the wire.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution
Solution: The total flux is 4`pi kq, where q is the total charge 5.9 `microC. This flux is 4`pi (9 x 10^9 N m^2/C^2 ( 5.9 `microC)) = 667200 N m^2/C.
The total surface area of the cylinder is 29 meters (2`pi ( .2100 m))) = 38.26 m^2.
The magnitude of the electric field is flux / area = ( 667200 N m^2 / C) / ( 38.26 m^2 ) ) = 17430 N / C.
At a distance of .05000 meters from the wire, the flux would be evenly spread over a cylinder 29 m long and with radius .05000 meters. The area of this cylinder would be 29 meters (2`pi ( .05000 m))) = 9.110 m^2. The electric field would therefore be flux / area = ( 667200 N m^2 / C) / ( 9.110 m^2) = 73230 N / C.
Generalized Response: A total charge Q will produce flux 4 `pi k Q. If the charge is evenly distributed on a wire of length L, then a cylinder of radius r and length L will have total area 2 `pi r L on its curved surface. If the cylinder is uniformly penetrated by all the flux produced by the charge, the flux density on this curved surface will be flux / area = 4 `pi k Q / (2 `pi r L) = 2 k Q / (r L). This can be written as 2 k (Q/L) / r, or 2 k `lambda / r, where the Greek letter `lambda is the charge / unit length along the wire.
.
.
.
.
.
.
.
.
.
.
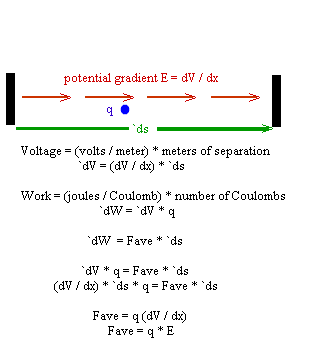
Figure description: The figure below shows a charge q moving through a displacement `ds in the direction of a potential gradient dV / dx. The potential difference will be the product of the potential gradient and the displacement: `dV = dV / dx * `ds. The work done on the charge is therefore `dW = q `dV; this work is also the product `dW = Fave * `ds of the average force on the charge and the displacement. Setting these two expressions for work `dW equal we arrive at the conclusion that Fave = q dV/dx = q E.
E = dV / dx is called the electric field. Since E = Fave / q, we see that the electric field E is the force per unit charge experienced by a charge.