Problem: Find symbolic expressions for the following:
The total area of an open cylinder of length L and radius r which symmetrically surrounds a uniform charged conducting wire of length L.
The total flux generated by a charge Q distributed uniformly on the wire.
The electric field at distance r from the wire.
The work done to move a charge dq from distance r1 to distance r2 from the wire, as approximated by the assumption that the electric field is uniformly equal to the field at the midpoint distance.
The work required per unit charge to move the charge from distance r1 to distance r2 from the wire, using the same approximation as before.
Use your expressions to find the following:
The electric field at a distance of 1.321 meters from a uniform charge of 754 `microC on a wire 95.4 meters long, at a point 3.2 meters from the wire and not close to either end.
The approximate energy required to move a charge of 1.594 `microC from a distance of .2000 meters to a distance of 3.200 meters from the wire, based on a midpoint estimate of the field.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution
Solution: The total area of the cylinder is the product of its length L and its circumference 2`pi r, or area = 2`pi r L.
The total flux is 4`pi kQ, so the electric field is
E = flux / area = 4`pi kQ / (2`pi r L) = 2kQ / (r L).
Note that this can be written as 2 k (Q/L) / r, where Q/L is the charge per unit length, called the 'line density' of the charge distribution.
The midpoint distance is rMid = (r1 + r2) / 2; the distance moved is dr = r2 - r1. The approximate work is equal to the product of the force exerted by the field at distance rMid and the distance dr.
The electric field at rMid is Emid = 2k (Q/L) / rMid, so the force on a charge dq is
F = q Emid = 2k dq (Q/L) / rMid.
Multiplying this force by the distance dr we obtain
W = F dr = 2k dq (Q/L) dr / rMid.
Since rMid = (r1+r2)/2 and dr = (r2-r1), we see that
W = 2k dq (Q/L) (r2 - r1) / [(r2+r1)/2] = 4k dq (Q/L) (r2-r1)/(r2+r1).
At 1.321 meters, the 754 `microC charge will create an electric field of magnitude
2k (Q/L) / r = 2k ( 754 `microC / ( 95.4 m) ) / ( 1.321 meters) = 2(9 x 10^9 N m^2/C^2) ( 7.903 x 10^-6 C / m) / ( 1.321 m) = 53840 N/C.
The midpoint between the .2000 m distance and the 3.2000 meter distance is at a distance of rMid = 1.7 meters from the wire. The distance moved is 3 meters, so the midpoint approximation to the work done in moving the charge dq = 1.594 `microC is
W = 2k ( 1.594 `microC) ( 754 `microC / ( 95.4 m) / 1.7 m ) * 3 meters = Joules
Generalized Solution
Generalized Response:
.
.
.
.
.
.
.
.
.
.
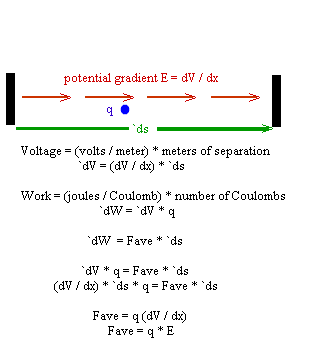
Figure description: The figure below shows a charge q moving through a displacement `ds in the direction of a potential gradient dV / dx. The potential difference will be the product of the potential gradient and the displacement: `dV = dV / dx * `ds. The work done on the charge is therefore `dW = q `dV; this work is also the product `dW = Fave * `ds of the average force on the charge and the displacement. Setting these two expressions for work `dW equal we arrive at the conclusion that Fave = q dV/dx = q E.
E = dV / dx is called the electric field. Since E = Fave / q, we see that the electric field E is the force per unit charge experienced by a charge.