Problem: A charge of 7 `microC is located at the origin, and a charge of 36 `microC is located at the point ( 84 m,0,0). The first charge is attached to a large mass, so that it can be considered stationary. The second charge is attached to a mass of 4 kg. Estimate, based on the force at the initial and final points, the work requird to move the second charge to the point ( 59.64 m,0,0) and the potential energy change associated with moving the second charge to this point.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The force at the original point is found from Coulomb's Law to be (9 x 10^9 N m^2/C^2)( 7 x 10^-6 C)( 36 x 10^-6 C)/( 84)^2 = .0003178 N. The force at the second point is found from Coulomb's Law to be (9 x 10^9 N m^2/C^2)( 7 x 10^-6 C)( 36 x 10^-6 C)/( 59.64 m)^2 = .0006306 N. The average of these forces is .0004742 N. Assuming this to be the average force on the charge over the interval between the points (it is not in fact equal to the average; it is higher than the average, but the average gives us a reasonable approximation in this case), we find the work from this force and the displacement from the first point to the second. The displacement is ( 84 m - 59.64 m) = 24.36 m. The force that moves the charge from 59.64 meters to 84 meters is equal and opposite to the force on the charge, or to + .0004742 N. This is the force that does the work. So the work done is ( 24.36 m)( .0004742 N) = .0115 Joules. This work, if positive, could be recovered in the form of kinetic energy if the particle was released. If negative, it could have been done at the expense of an equal amount of kinetic energy.
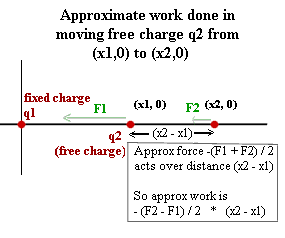
Generalized Response: As a charge q2 is moved from distance r1 = x1 to distance r2 = x2 from a fixed charge q1, the force on the charge changes from F1 = k q1 q2 / r1^2 to F2 = k q1 q2 / r2^2. This change is not linear, so the average force exerted is not the average of F1 and F2; however if the forces are not too different the average of the forces gives a reasonable approximation of the average force. Using (F1 + F2) / 2 as the approximate average force, we obtain an estimate of the work done when we multiply the force opposite to this average force by the displacement `dr = r2 - r1= x2 - x1 to obtain
approximate W = -(F1 + F2) / 2 * (r2 - r1) = -(F1 + F2) / 2 * (x2 - x1).
.
.
.
.
.
.
.
.
.
.
Figure description: The figure shows the charge q2 at positions (x1,0) and (x2,0), and the forces F1 and F2 at those points (assuming a force of attraction; if the charges are of the same sign the forces will be forces of repulsion). The force required to move the charge from x1 to x2 will be in the direction opposite to F1 and F2. If we use (F1 + F2) / 2 as the approximate average force over the interval, we must therefore apply an approximate average force of -(F1 + F2) / 2 over distance (x2 - x1), obtaining the indicated work.