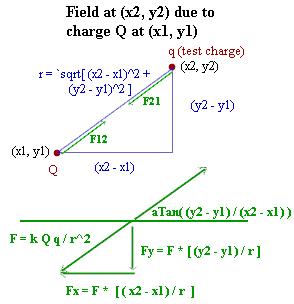
Problem: What are the magnitude and the direction (in degrees) of the electric field at the point ( 3 m, 3 m), due to a charge of 13 `microC at ( 6 m, 12 m)?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution: The electric field at a point is the force per unit test charge, with the test charge located at the point. So we assume a unit test charge. The force on the test charge is one of repulsion, so will be in the direction from ( 6, 12) to ( 3, 3). The distance between charges is `sqrt[( 3- 6)^2+( 3- 12)^2] m = 9.486 m. The magnitude of the force is (9 x 10^9 N m^2/C^2)( 13 x 10^-6 C)(1 C)/( 9.486 m)^2 = 1300 N. The x and y displacements from charge 13 `microC to the 1 C test charge are, respectively, -3 m and -9 m, so the x and y components are in proportion -3/ 9.486, and -9/ 9.486 to the force. The x and y forces are therefore ( 3/ 9.486)( 1300 N) = -411.0 N and ( 9/ 9.486)( 1300 N) = -1233 N. Since these are the forces on a 1 C test charge, the electric field has components -411.0 N/C and -1233 N/C in the x and y directions, respectively. The resultant force therefore has magnitude `sqrt[( 411.0 N/C)^2+( 1233 N/C)^2] = -1299 N/C. Its direction is arctan( -9/ -3) = -288 degrees, after correcting the calculated arctangent, which gives 72 deg, for the quadrant of the vector.
Generalized Response: We imagine charges Q and q at respective positions (x1, y1) and (x2, y2) in the plane, with q the 'test charge'. We find the force per unit charge on q.
By the usual means,we find that the force on either charge is F = k Q q / r^2. The force F12 exerted on charge 1 by charge 2 is equal and opposite to the force F21 exerted on charge 2 by charge 1.
The angle of the force is either
aTan( (y2 - y1) / (x2 - x1)) or
aTan( (y2 - y1) / (x2 - x1)) + 180 deg,
depending on whether F is repulsive (F positive) or attractive (F negative).
.
.
.
.
.
.
.
.
.
.
Figure description: The figure below depicts the charges Q and q as attracting charges at points (x1,y1) and (x2,y2). The legs and hypotenuse of the fundamental triangle are indicated (the hypotenuse is found using the Pythagorean Theorem; the legs are found by the obvious means). The force vectors F12 and F21 are depicted, assuming an attractive force resulting from opposite charges. The second figure shows the force vectors F21 and F12. F12 makes angle aTan( (y2 - y1) / (x2 - x1) ) with the x direction; since the force is of attraction we see that F21 is in the opposite direction, at angle aTan( (y2 - y1) / (x2 - x1) ) + 180 deg.